震相走时的计算是地震学的基本问题之一。

目前，计算一维分层模型下的震相走时，主要使用两个程序包：ttimes 和 TauP。 ttimes 相对来说有些古老，所以多数情况下更推荐使用 TauP。但 TauP 不支持 PKPab、 PKPbc 这种震相名，所以偶尔可能还是需要使用 ttimes。

ttimes 和 TauP 都是根据 Buland and Chapman（BSSA,1983）提出的理论框架来实现的， 本文是对这篇文章的核心内容的简单总结。

提出问题

给定一维水平分层模型，若震源位于地表，要求计算某一震相（如 P 波）在特定震中距 （如 50 度）处的震相走时。

说明：

  1. 球状分层模型和水平分层模型下的理论公式基本相同，只是个别变量需要做 简单替换，这里用更简单的水平分层模型；
  2. 震源位于地表或地下，只会影响到积分的上下限，这里为了简化，将震源放在地表；
  3. 这里以简单的 P 波为例，理论上是可以算各种复杂路径的震相的；

基本公式

对于一个速度仅是深度的函数的一维分层速度模型 $v(z)$，其慢度为

$$u(z) = \frac{1}{v(z)}$$

定义射线参数（即水平慢度）为

$$p = \frac{\sin(i(z))}{v(z)}$$

其中 $i(z)$ 是射线与垂直方向的夹角。垂直慢度为

$$\eta(p, z) = (u^2(z)-p^2)^{\frac{1}{2}}$$

在做了如上定义后，对于从地表发出的任意一条射线参数为 $p$ 的射线，即可计算出 该射线所对应的走时和震中距 (Introduction to Seismology, Peter Shearer, 公式 4.31-4.32 及之间的推导)：

$$T(p) = 2\int_0^{z_p} \frac{u^2(z)}{\eta} dz$$

$$X(p) = 2p\int_0^{z_p}\frac{dz}{\eta}$$

其中 $z_p$ 是射线的反转点（turning point）的深度。

另一个重要的公式是：

$$p = \frac{dT}{dX}$$

基本解法

有了上面的几个公式，基本就可以有一个直观暴力的解法了。

对于任一射线参数 $p$，都可以找到射线的 $z_p$，然后即可积分计算该射线所对应的 震中距 $X(p)$ 和走时 $T(p)$。

但是问题中要计算的是特定震中距 X0 的走时，那么就可以对射线参数进行遍历，每给 一个射线参数，就计算一个震中距 X(p)，若 X(p)>X0，则把射线参数改大一些， 若 X(p)<X(0)，则把射线参数改小一些。最终，总可以找到一个射线参数，使得 X(p) 和 X0 几乎相等。

这基本就是一个二分查找，实现起来也很简单。但此方法的问题在于，假定了 X(p) 是 p 的 单调递减函数，而真实地球模型中有低速层和高速不连续面，会出现三叉波和影区，不 符合单调递减函数的假设。在同一个震中距处可以有多个射线参数。

因而这里的思路仅适用于某些简单的震相，比如 P、PcP、PKiKP 之类。

tau(p)函数

定义 delay-time 函数 $\tau(p)$：

$$\tau(p) = T(p) - pX(p)$$

简单推导可知，tau 函数可以用如下公式计算：

$$\tau(p) = 2\int_0^{z_p} \eta dz$$

且其具有如下性质：

$$\frac{d\tau}{dp} = \frac{dT}{dp} - X(p) - p \frac{dX}{dp} = \frac{dT}{dX}\frac{dX}{dp} - X(p) - p \frac{dX}{dp} = -X(p)$$

由于 X(p) 是震中距，为非负值，因而，$d\tau/dp$ 是个非正值。即函数 $\tau(p)$ 的 斜率是非正值，因而 tau 函数是一个单调递减函数，即对任意一个射线参数 p，都有唯一的 tau。

theta(p,x) 函数

进一步定义 theta 函数：

$$\theta(p,x) = \tau(p) + px$$

再看看前面 tau 函数的定义：

$$T(p) = \tau(p) + pX(p)$$

theta(p,x) 和 T(p) 看上去很相似，但需要特别注意的是，T(p) 是 p 的函数，而 theta 是 p 和 x 的函数。即在 T(p) 的定义中，X(p) 是射线 p 所对应的震中距，具有唯一或唯 N 个值； 而 theta 函数中，x 是一个任意的变量，理解这一点很重要。

theta 函数对 p 求偏导，可得：

$$\frac{\partial \theta}{\partial p} = \frac{d\tau}{dp} + x = x - X(p)$$

因而，若在某个 p0 处，有 theta 函数对 p 的偏导为零，则有 x=X(p0)，进而有：

$$T(p_0) = \tau(p_0) + p_0 X(p_0) = \theta(p_0, X(p_0))$$

上面的公式表明：若某个 p0 处，theta 函数对 p 的偏导为零，则该射线参数 p0 所对应的 theta 值就是射线的走时 T(p0)。

下图是一个比较直观的例子（Chapman, 1978, GJI, Figure 12）。对于存在高速区的情况， 走时曲线中会出现三叉波，如左上图 T(X) 曲线所示。左下图中给出了 tau(p) 曲线，是一个 单调递减曲线。对于震中距 A、B、C、D，分别计算了其对应的 theta 曲线，如右边四张图所示。

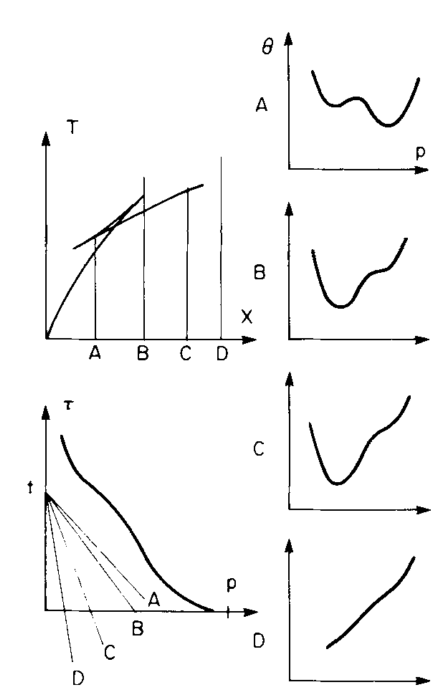
  • 对于震中距 A，从 theta 曲线中可以看出，该曲线有三个局部极值，因而在震中距 A 处， 有三条射线参数不同的射线，在不同的时间抵达震中距 A；
  • 对于震中距 B，左边有一个明显的局部极值，右边有一小段，theta 曲线近似为平的， 这意味着，存在某段射线参数，其到震中距 B 的走时基本是一样的。这一点一般称为 caustic，在射线理论中，这里的振幅是无穷大的。
  • 对于震中距 C，有一个局部极值点；
  • 对于震中距 D，无局部极值点；

总之，对于特定震中距，计算出 theta 曲线后，从曲线中很容易看出在该震中距处有哪些 射线在何时到达，这也是 WKBJ 理论地震图计算方法的基本原理的一部分。

高级解法

有了上面的 theta 函数及其性质作为理论基础，就可以顺畅的解决上面的问题了。

基本步骤如下：

  1. 读取速度模型，计算得到慢度模型
  2. 对 p 做遍历，计算得到离散的 tau(p) 函数
  3. 计算特定震中距 X0 处的 theta(p,x)，即 theta(p,X0)，或表示为 theta(p)
  4. 寻找 theta(p) 对 p 的偏导为零的点，即 theta(p) 的局部极值点
  5. 每个极值点处射线参数 p0 即为符合要求的射线参数，而 theta(p0) 则为要计算的走时

其他细节

上面总结了计算走时的理论框架，实际数值计算时还甚至到更多的细节，具体参考 1983 那篇文章的后面部分。

  1. tau(p) 积分的计算
  2. 震源深度的处理
  3. 极值的寻找
  4. 震相名的解析
  5. …

参考文献

  1. Chapman, C. H. (1978). A new method for computing synthetic seismograms. Geophysical Journal International, 54(3), 481-518.
  2. Shearer, P. M. (2009). Introduction to seismology. Cambridge University Press.
  3. Buland, R., and Chapman, C. H. (1983). The computation of seismic travel times. Bulletin of the Seismological Society of America, 73(5), 1271-1302.