pssac 使用教程
文章目录
注意:本文仅针对 Prof. Lupei Zhu 的 pssac 程序,其仅可在 GMT 4下使用。
对于GMT5用户,GMT 在 5.3.1 之后自带了 pssac,可以使用 gmt pssac 直接调用。
相关文档见:
- http://gmt.soest.hawaii.edu/doc/latest/supplements/meca/pssac.html
- http://modules.gmt-china.org/pssac
pssac 可以读取 SAC 波形数据,并利用 GMT 的绘图功能将波形数据绘制在 PS 文件中。
pssac 绘制的波形图,大致可以分为三类:
- 波形振幅图:横轴是时间,纵轴是振幅;
- 剖面图:横轴是时间,纵轴是其他物理量(比如震中距、方位角、反方位角以及文件号);
- 任意位置图:将波形文件绘制在图上的任意位置;
本文首先简单介绍 pssac 的各个选项,然后依次介绍如何绘制波形振幅图、剖面图以及任意位置图,在这个过程中会详细介绍较复杂的选项。
选项一览
终端输入 pssac 即可得到 pssac 的使用说明。pssac 的命令中主要包含了三个部分:
- GMT 的标准选项
- pssac 的特有选项
- SAC 文件
GMT 标准选项
pssac 继承了 GMT 的众多标准选项,包括:
- 必须选项:
-J -R - 可选选项:
-B -K -O -U -X -Y -W
这些选项的具体用法可以参考 GMT 官方文档,简单说明如下:
-J:设置投影方式以及底图尺寸;-R:设置横纵坐标的范围;-B:设置底图边框的属性;-K -O:图层叠加;-U:Unix 时间戳;-X -Y:移动绘图原点;-W:用于设置线条的粗细、颜色与线型;
需要注意: pssac 不支持 -P 选项。
pssac 特有选项
pssac 的特有选项有:
-C -E -G -I -M -N -Q -r -S -V
先简单介绍一个这些选项的作用:
-I:绘图之前先对波形做积分;代码中在做积分时,没有乘以采样间隔,因而导致波形的绝对振幅有误,但波形的形状是正确的;-Q:绘图之前先对波形做平方;-r:绘图之前先去除均值;该选项仅在同时使用-M选项时有效;-Nclip:使用该选项会使得波形振幅限制在[-clip, clip]范围内;若波形数据中某数据点的振幅值大于 clip,则该数据点会被赋值为 clip;若某数据点的振幅值小于 - clip,则该数据点会被赋值为 - clip;该选项仅在同时使用-M选项时有效;-Gr/g/b/c:将振幅大于c的部分填色,颜色由r/g/b决定;此处只支持 RGB 颜色;不支持颜色名、HSV 等;-Ct1/t2:只截取波形中 t1 到 t2 时间段内的数据;若只使用-C而不给出 t1 和 t2,则会根据-R选项指定的 X 轴范围对数据做截取;-Msize/alpha:将波形数据振幅归一化到某个尺寸;-Sshift:将波形数据整体移动 shift 秒,相当于b=b+shift;-E:设置剖面图的 Y 轴类型,以及数据的时间对齐方式;-V:垂直绘制波形,即交换 X 轴和 Y 轴;
不同的选项对数据做了不同的处理,这就涉及到数据处理的顺序问题。前面的处理会影响到后面的处理,因而也会影响到其他选项的参数的选取。pssac 中波形的处理顺序,或者说不同选项之间的优先级:
先处理 X 轴:
波形对齐 (-E) => 波形整体 shift(-S) => 截窗 (-C)再处理 Y 轴,即波形发生了变化:
积分 (-I) => 平方(-Q) => 去均值(-r) => 振幅归“一” 化(-M) => 限幅处理(-N)交换 X 轴和 Y 轴(-V)
绘制波形:
绘制波形 (-W) => 填色 (-G)
波形振幅图
这一节会介绍如何用 pssac 绘制最简单的波形振幅图,在介绍的同时会尽可能详细地解释每个选项的意义。在绘制简单的波形振幅图时不需要使用 -E 选项,所以 -E 选项的介绍放在绘制剖面图时再介绍。
示例 SAC 数据
先用 SAC 生成两个示例数据,以方便重复下面的绘图:
SAC> fg seis
SAC> rmean
SAC> ch t0 12 // 做了 t0 标记,供后面使用
SAC> w seis.1
SAC> mul 2 // 将数据整体乘以 2,写到新文件中
SAC> w seis.2
用 saclst 查看一下两个数据的头段信息:
$ saclst b e t0 depmax depmin f seis.?
seis.1 9.46 19.45 12 1.61919 -1.47073
seis.2 9.46 19.45 12 3.23837 -2.94147
单个波形的振幅
先以 seis.1 为例,根据头段信息可知,该数据的时间范围为 [9.46,19.45],
振幅范围为 [-1.47,1.62] 。据此,可以设置 - R 选项的参数为 -R9/20/-2/2
:
pssac -JX20c/10c -R9/20/-2/2 seis.1 > test.ps

上面的例子中只使用了 - J 和 - R 选项,是 pssac 的最小示例。通常情况下,还需要使用 - B 选项给波形图加上边框:
pssac -JX20c/10c -R9/20/-2/2 -B1:"T(s)":/0.5:"Amplitude":WSen seis.1 > test.ps
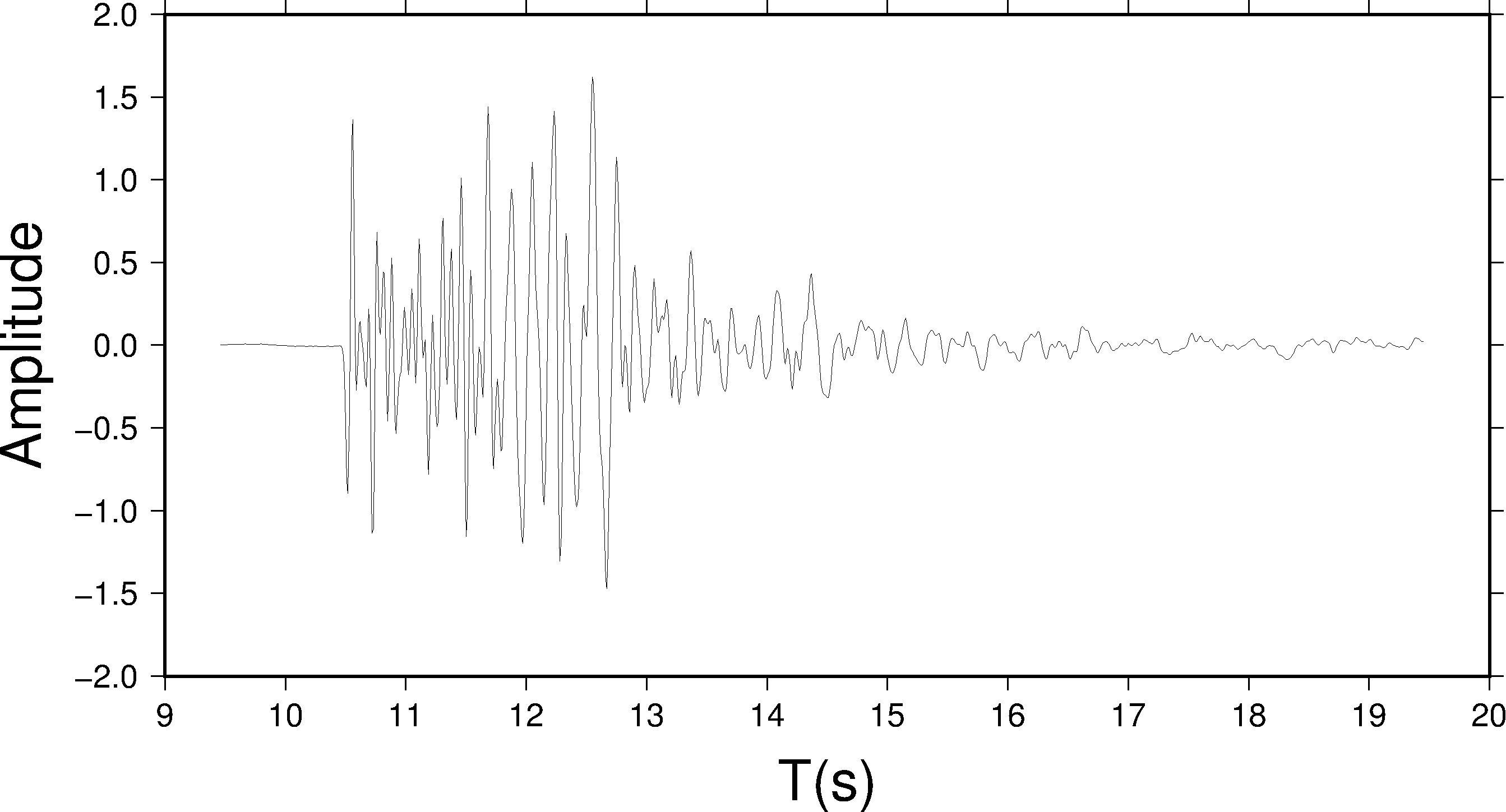
加上边框之后就很清楚了,横轴表示时间,纵轴表示波形的绝对振幅。
绘制多个波形
绘制一个波形是不够的,pssac 还可以一次性绘制多个波形:
pssac -JX25c/5c -R10/16/-3.2/3.2 -B1:"T(s)":/1:"Amplitude":WSen seis.? > test.ps
这个例子中,同时绘制了 seis.1 和 seis.2 两个波形,为了看上去更明显,这里使用了稍稍不同的 - J 和 - R。可以看到 seis.2 和 seis.1 共用了 X 轴和 Y 轴,跟 SAC 中的 plot2 命令的效果相同。
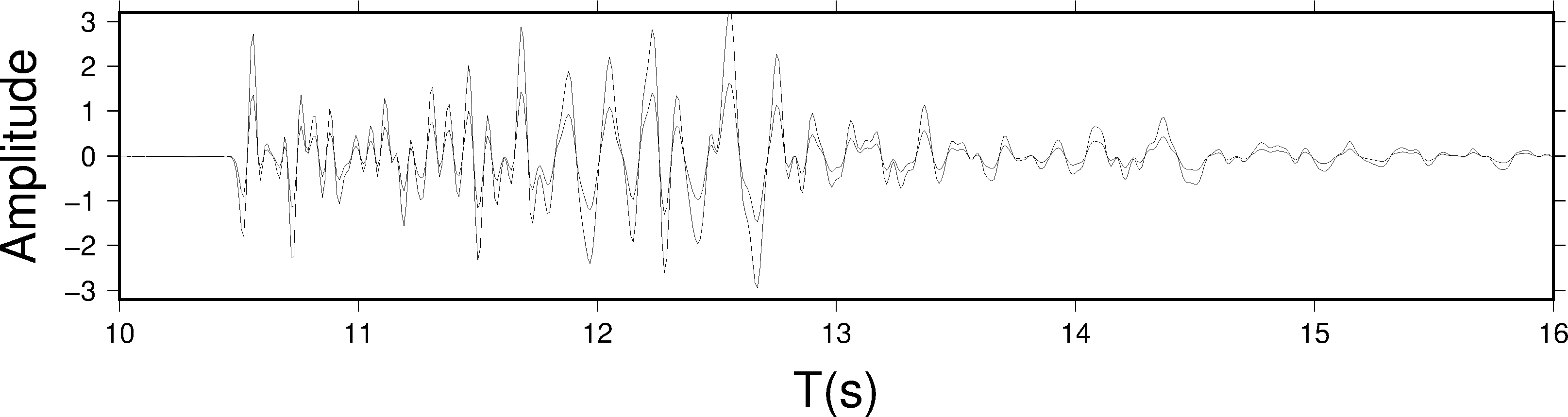
-S 选项的效果
-S 选项相当于将数据的 b 值加上了 shift 秒,因而会影响到 X 轴的范围,即影响到 - R 选项的参数:
pssac -JX20c/10c -R29/40/-2/2 -B1:"T(s)":/0.5:"Amplitude":WSen -S20 seis.1 > test.ps
上面的代码中使用了 -S20 ,将波形整体移动了 20 秒,此时移动后的波形 b=29.46, e=39.45 ,因而 -R 选项也要相应的变化。
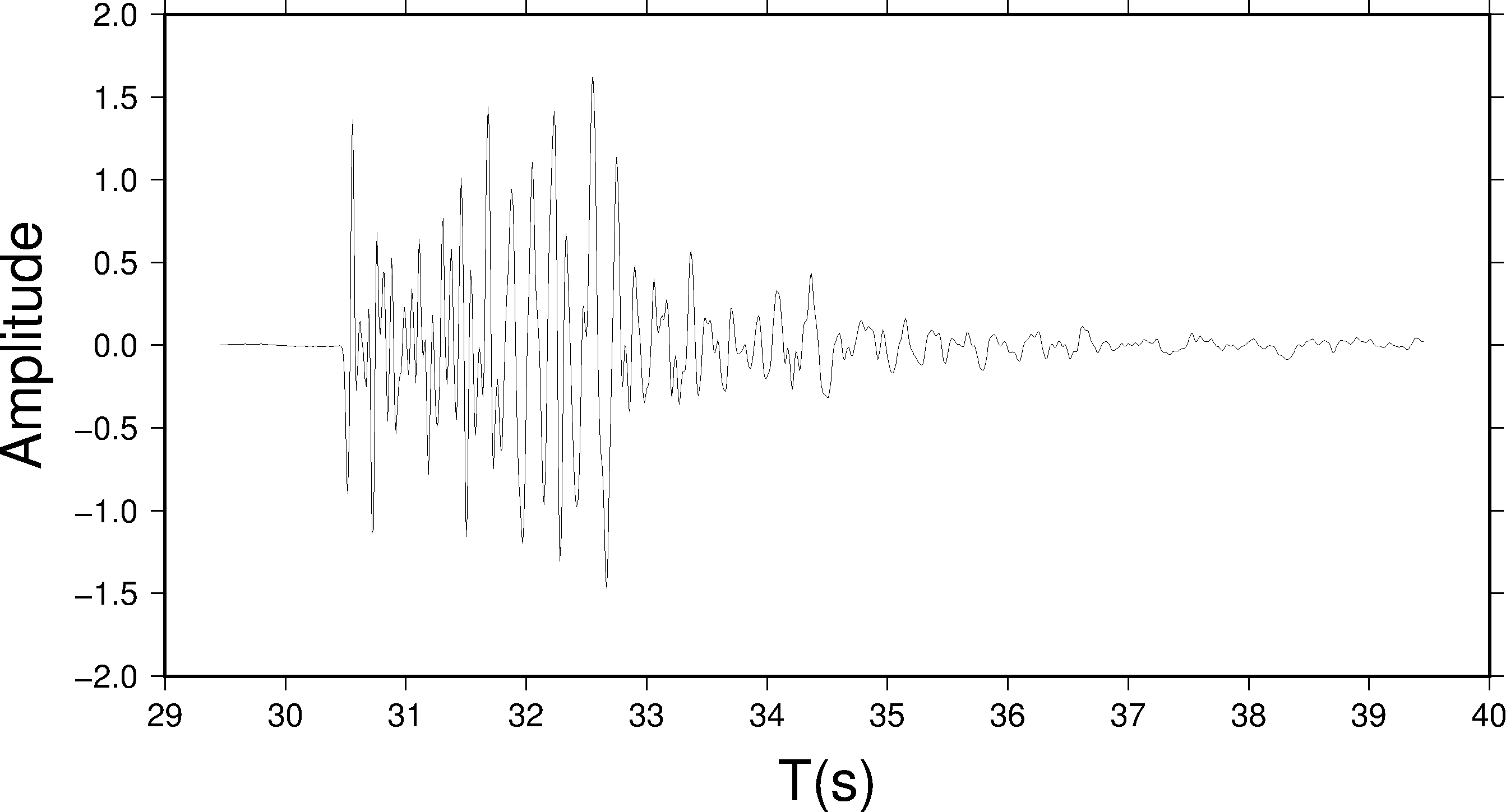
-C 选项的效果
-C 选项的作用在于从当前数据中截取其中一段,这样可以只显示一个长波形中的一小段:
pssac -JX20c/10c -R9/20/-2/2 -B1:"T(s)":/0.5:"Amplitude":WSen -C11/14 seis.1 > test.ps
本例中,数据的时间范围是 [9.46, 19.45], -C 选项截取了其中的 11 到 14 秒,用于绘图,效果图如下,注意与图 2 对比。
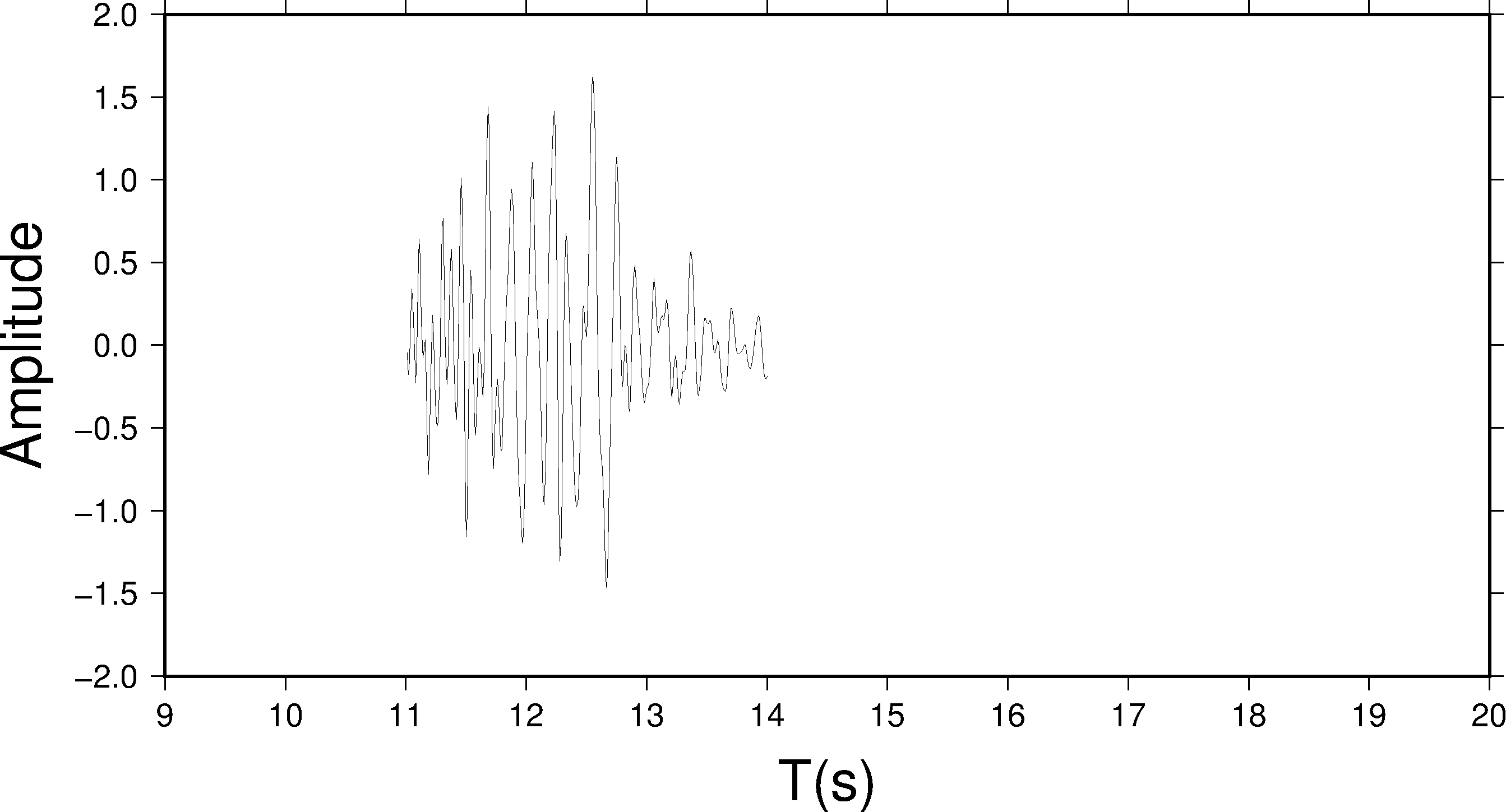
由于 -S 选项优先于 -C 选项,因而使用 -S 选项会对 -R 和 -C 的参数同时产生影响:
pssac -JX20c/10c -R29/40/-2/2 -B1:"T(s)":/0.5:"Amplitude":WSen seis.1 -S20 -C31/34 > test.ps
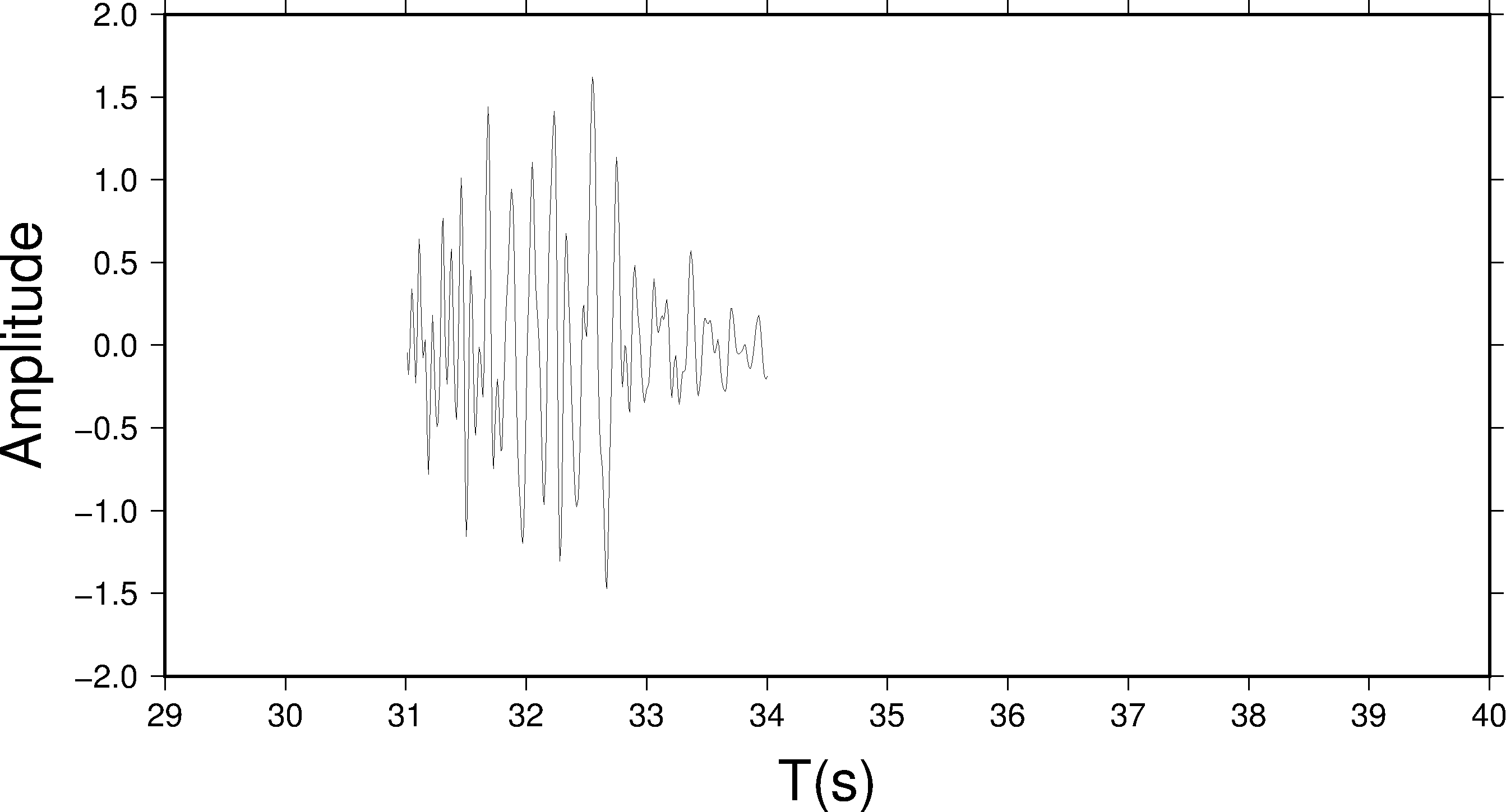
本例中,同时使用了 -S 和 -C ,由于 -S 优先于 -C,所以波形数据的时间范围首先被 -S20 选项从 [9.46, 19.45] 移动到 [29.46, 39.45] ,而 -C31/34 则截取了偏移后的波形数据的 31 到 34 秒,相当于截取偏移之前数据的 11 到 14 秒。
-I, -Q, -r
三个选项分别实现波形的积分、平方和去均值,加上这些选项后会影响波形的振幅,因而需要调整 - R 中 Y 轴的范围。另外需要注意的是,-C 选项的优先级要高于这三个选项,因而若同时使用了 -C 选项,则只会对截取的这一段数据做积分 / 平方 / 去均值的操作。这几个选项相对简单,且不常用,暂且不多说。
-M 选项
-M 选项会对波形进行 “归一化”,只是这里的“归一化” 并不真的代表将振幅归一化到 1。
-M 选项的语法为 -Msize[/alpha],依据参数的不同可以进一步分为三种用法。
-Msize-Msize/alpha(alpha<0)-Msize/alpha(alpha>0)
-M 选项多用于剖面图中,很少用于波形振幅图中,但本质上是没有区别的,故而在这里一并介绍。
-Msize
size 的单位是英寸,这种用法会使得所有波形的最大振幅差在图上的长度为 size 英寸。其中,最大振幅差是指波形的最大振幅值与最小振幅值的差的绝对值,即 abs(depmax-depmin) 。
pssac -JX6i/5i -R9/20/-2.5/2.5 -B1:"T(s)":/0.5g0.5:"Amplitude":WSen -M2 seis.? > test.ps
这个例子中, -M2 将所有波形做归一化使得最大振幅差对应的高度为 2 英寸。由于 Y 轴的范围是 [-2.5, 2.5],Y 轴的高度为 5 英寸,即图上 1 个 Y 单位所对应的长度为 1 英寸,因而归一化之后最大振幅差对应 2 英寸,即 2 个 Y 单位,从图中也可以很明显的看出来。
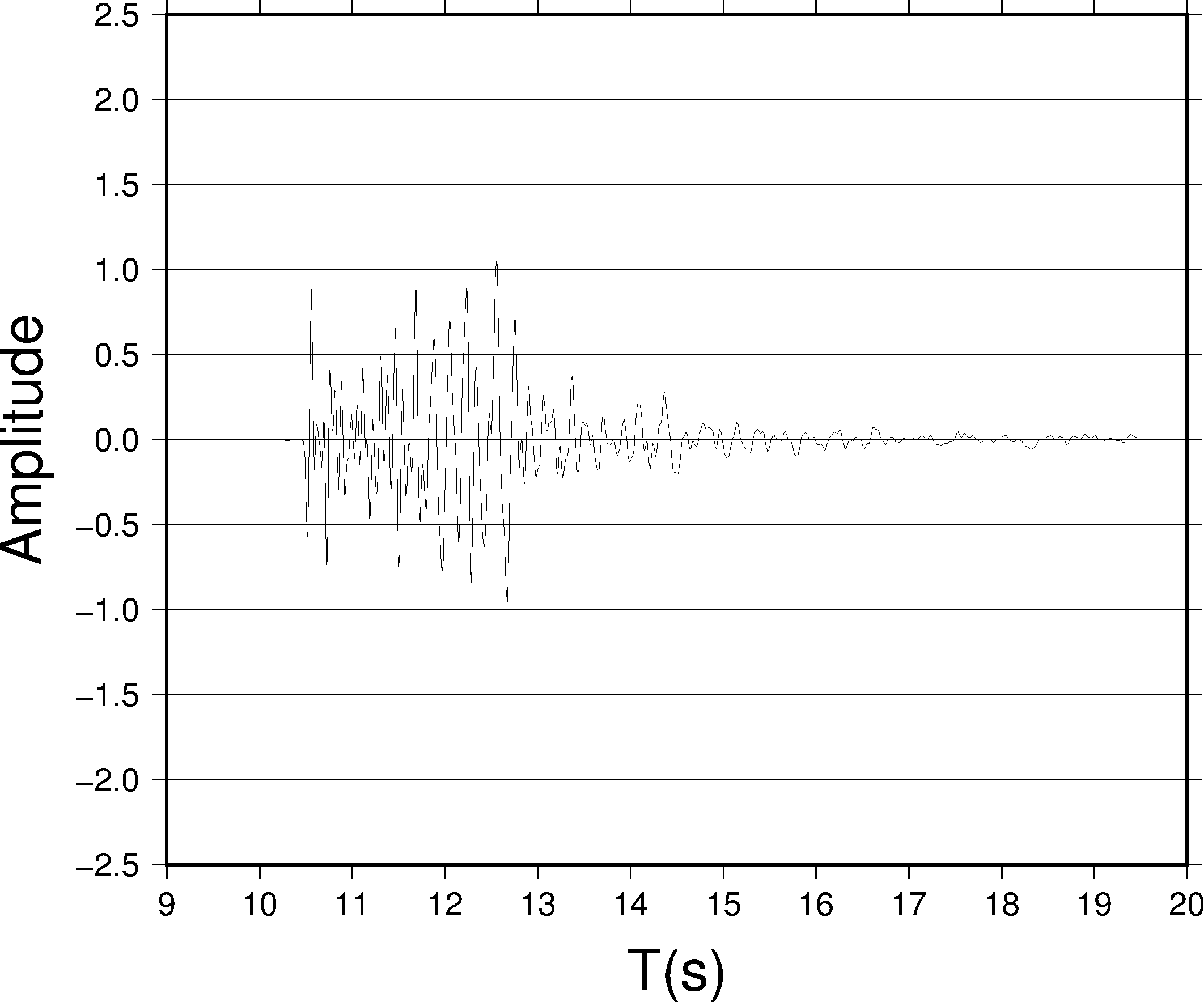
这种做法使得所有波形在图上看上去最大振幅差都是 size 英寸,因而所有波形都失去了绝对振幅和相对振幅信息。以这个例子为例,图中读出的振幅值已经不再是波形真实的振幅值,即丢失了绝对振幅;另一方面,本例中绘制了 seis.1 和 seis.2 两个 SAC 文件,尽管两个 SAC 文件的振幅有两倍的差距,归一化之后相对振幅信息丢失,所以看上去两个波形完全重合了。
alpha 小于 0
若 alpha<0,则会根据第一个波形数据计算归一化因子,使得第一个波形的最大振幅差在图上等于 size 英寸,而其余的波形则会乘以同一个归一化因子。因而这种做法,所有波形虽然失去了绝对振幅信息,但却保留了相对振幅信息。
alpha 大于 0
这种情况下,归一化因子为:
yscale = pow(abs(h.dist), alpha)*size
这样设计的原因是,对于一个正常的波形来说,震中距越大,由于几何扩散的效应,振幅越小。这个选项相当于对几何扩散项进行校正,即绘制了不考虑几何扩散情况下波形的相对振幅。
其中 alpha 是几何扩散因子,而 size 的含义不是太清晰。
-N 选项
-Nclip 选项会将绝对振幅超过 clip 的部分做截断。需要注意, -N 的优先级很低,因而 clip 值的选取要考虑其他选项对振幅的影响:
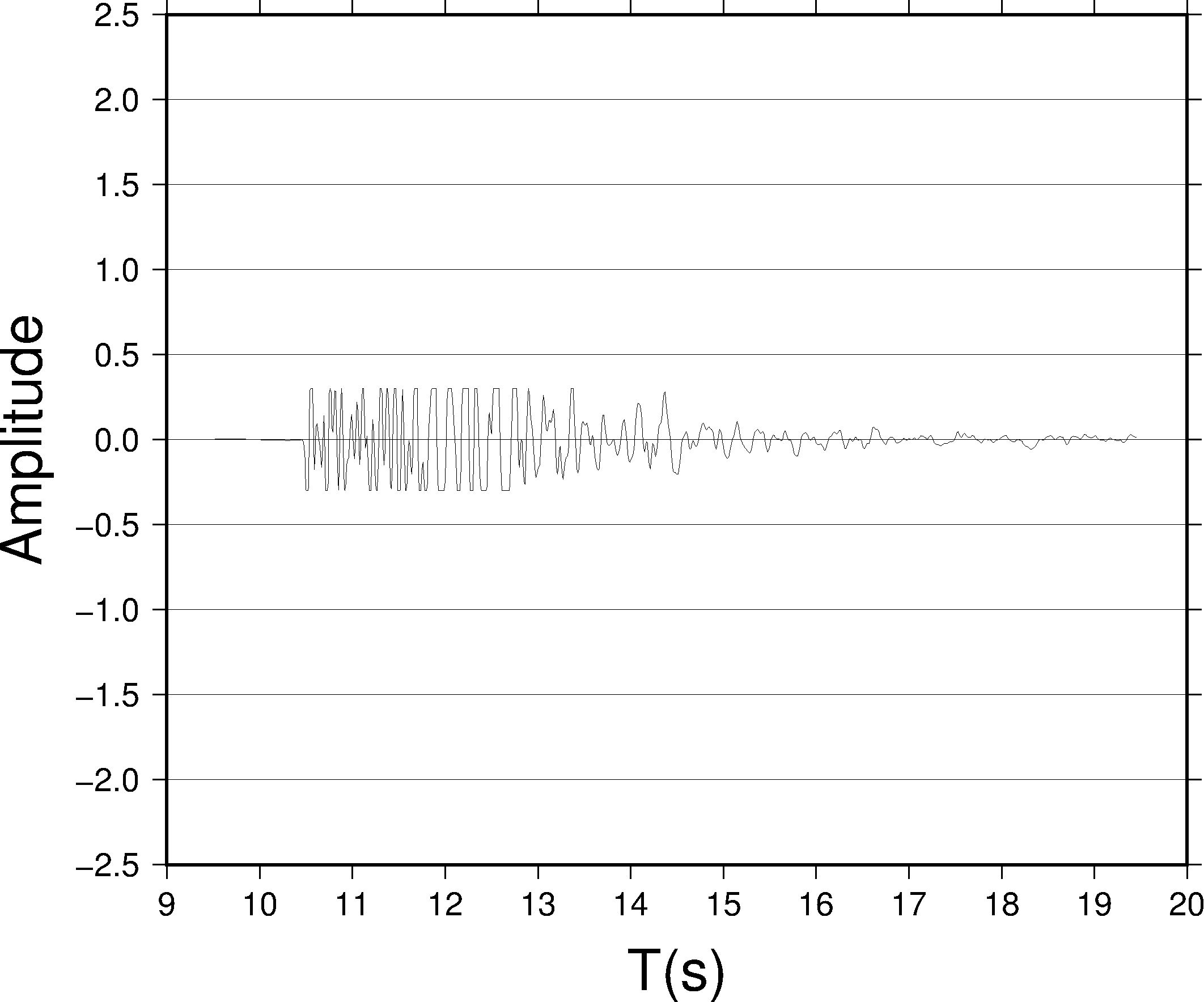
pssac -JX6i/5i -R9/20/-2.5/2.5 -B1:"T(s)":/0.5g0.5:"Amplitude":WSen -M2 -N0.3 seis.1 > test.ps
本例中,对绝对振幅超过 0.3 的部分做截断。此处的 0.3 是经过归一化之后的振幅值,因而没有明确的物理含义。
-V 选项
-V 选项会交换 X 轴和 Y 轴,因而 -J 、 -R 和 -B 都需要做相应修改:
pssac -JX5c/10c -R-2/2/9/20 -B1/2WSen seis.1 -V > test.ps
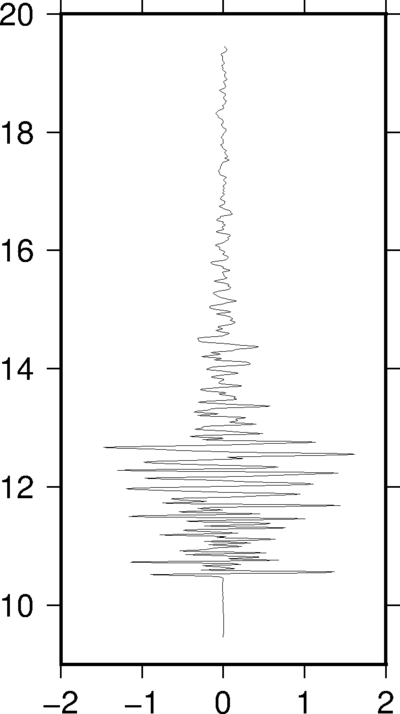
在某些特定的研究中会需要使用竖排模式。比如接收函数中,地震图中的某个震相到时可能与某个界面的深度成正比。通过将一系列波形竖排起来,纵坐标的时间对应某个特定的深度,因而可以很直观地看到界面深度的变化。
-W 和 - G 选项
-W 选项用于设置画笔数学,-G 选项用于控制波形的颜色填充:
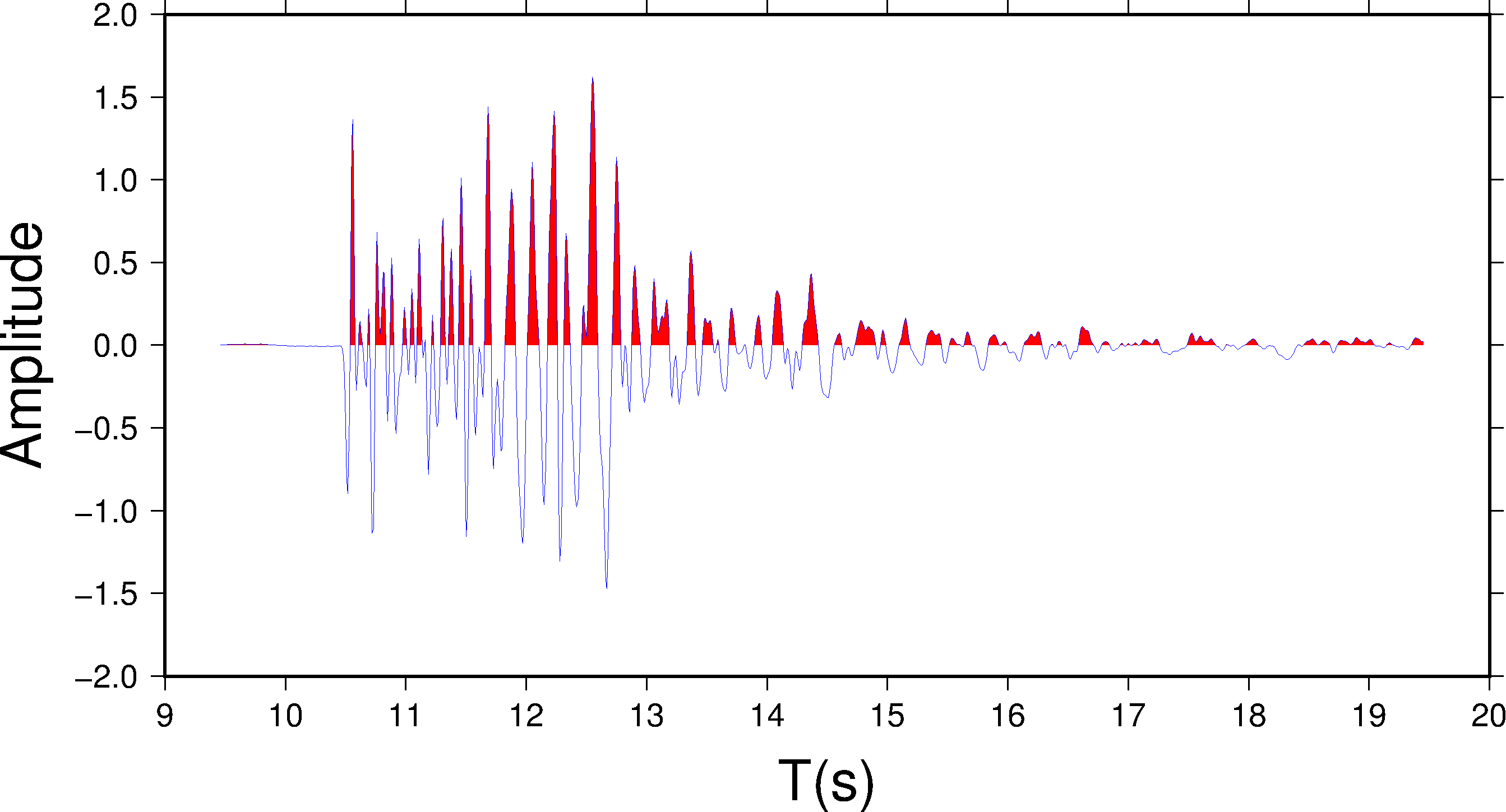
pssac -JX20c/10c -R9/20/-2/2 -B1:"T(s)":/0.5:"Amplitude":WSen -W0.2p,blue -G255/0/0/0 seis.1 > test.ps
本例中,线条宽度为 0.2p,颜色为蓝色,并对大于 0 的部分填充红色( 255/0/0)。
剖面图
剖面图:横轴为时间,纵轴为其他物理量,pssac 中纵轴可以是震中距、方位角、反方位角以及文件序号。
pssac 使用 -E 选择来指定剖面图的具体性质,同时用 -M 选项对多个波形做归一化。其他的选项参考前面的说明。
生成示例数据
先利用 SAC 自带的数据,生成绘制剖面图所需要的示例数据:
SAC> dg sub local cal.z cao.z cda.z cdv.z cmn.z cva.z cvl.z cvy.z
SAC> rmean
SAC> taper
SAC> bp c 0.5 3
SAC> w cal.z cao.z cda.z cdv.z cmn.z cva.z cvl.z cvy.z
查看一下这些文件的基本头段信息:
$ saclst b e a dist gcarc az baz f *.z
cal.z 9.99365 50.0089 20.5949 12.4876 0.112316 234.02 53.9503
cao.z 9.99365 50.0089 22.2028 23.0074 0.206933 144.09 324.182
cda.z 9.99365 50.0089 23.078 23.9117 0.215068 350.813 170.787
cdv.z 9.99365 50.0089 19.5975 5.4563 0.0490751 4.64117 184.644
cmn.z 9.99365 50.0089 20.6763 12.3995 0.111524 350.452 170.437
cva.z 9.99365 50.0089 20.7882 12.9964 0.116892 329.957 149.912
cvl.z 9.99365 50.0089 21.867 17.9895 0.161802 312.309 132.218
cvy.z 9.99365 50.0089 22.3656 18.8976 0.16997 318.278 138.192
波形振幅图
先用前面介绍过的方法,绘制一个波形振幅图。从数据的头段中可知,时间范围大概是 [10, 50] ,振幅的范围为 [-500,500] ,因而设置 - R 的范围为 -R9/55/-500/500 :
pssac -JX20c/10c -R9/55/-500/500 -B10/100WSen *.z > test.ps
此时,所有的波形共用 X 轴和 Y 轴,类似于 SAC 中 plot2 的绘图效果。
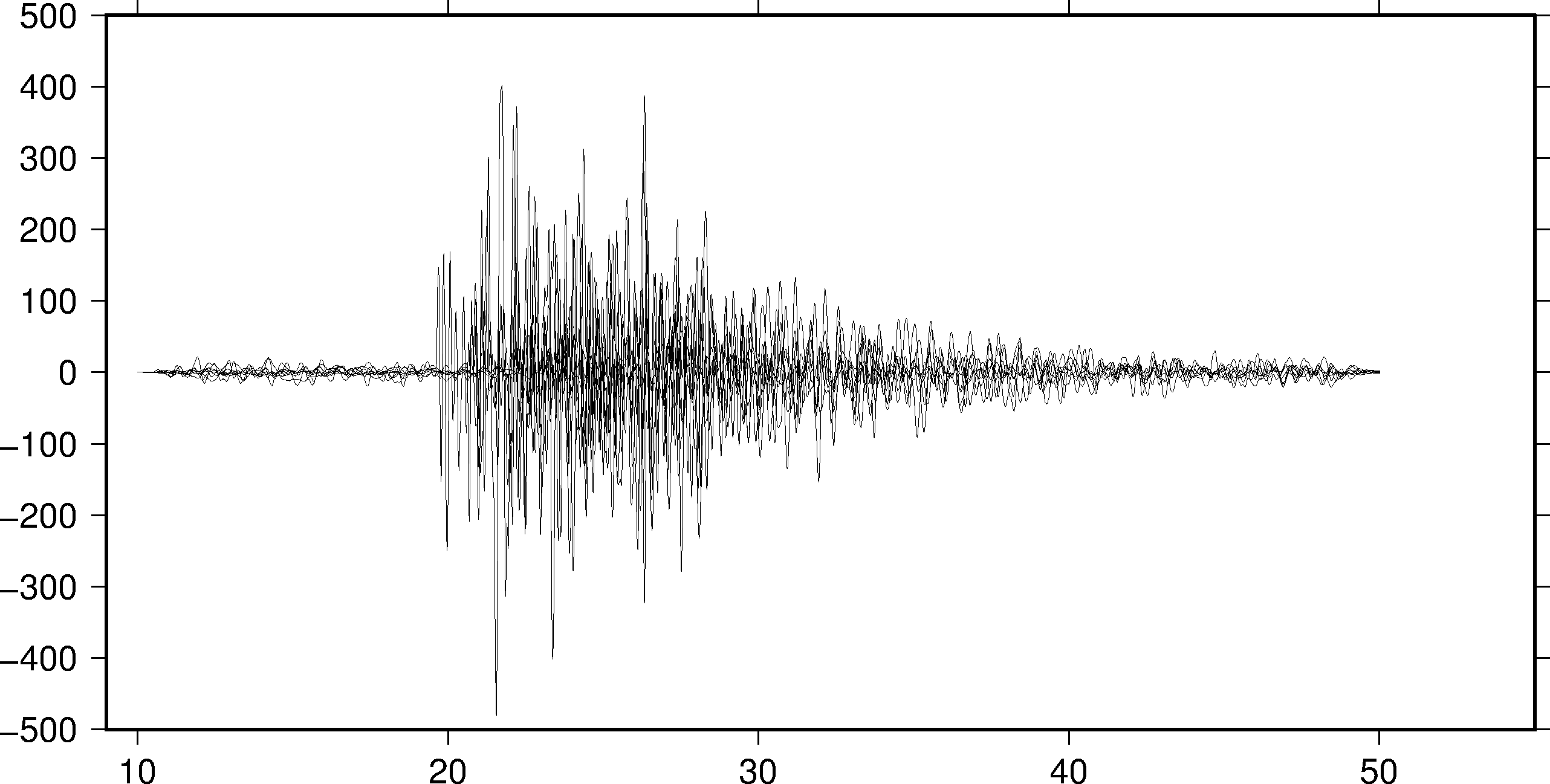
最简单的剖面图
-E 选项表明要绘制剖面图,其语法为 -E(k|d|a|n|b)(t[n]|vel)。语法中被小括号分开的两部分,分别用于指定剖面类型和时间轴对齐方式。
pssac 支持的剖面类型包括:
- a:Y 轴为方位角
- b:Y 轴为反方位角
- d:Y 轴为震中距(单位为度)
- k:Y 轴为震中距(单位为千米)
- n:Y 轴为波形的序号(从 1 到 N)
不同的剖面类型,对应的 Y 轴的范围就不同。下面的例子展示了不同的剖面类型所使用的命令,注意其中 -R 和 -B 选项的差异:
pssac -JX20c/10c -R10/50/3/28 -B10:"T(s)":/5:"Dist(km)":WSen -Ekt -M0.5 *.z > test.ps
pssac -JX20c/10c -R10/50/-50/380 -B10:"T(s)":/60:"Azimuth":WSen -Eat -M0.5 *.z > test.ps
pssac -JX20c/10c -R10/50/-50/380 -B10:"T(s)":/60:"Back Azimuth":WSen -Ebt -M0.5 *.z > test.ps
pssac -JX20c/10c -R10/50/0/0.25 -B10:"T(s)":/0.05:"Dist(degree)":WSen -Edt -M0.5 *.z > test.ps
pssac -JX20c/10c -R10/50/0/9 -B10:"T(s)":/1:"No.":WSen -Ent -M0.5 *.z > test.ps
这里只展示一下 -Ek 的结果,其他结果类似,此处 - M 的含义与之前介绍的相同。
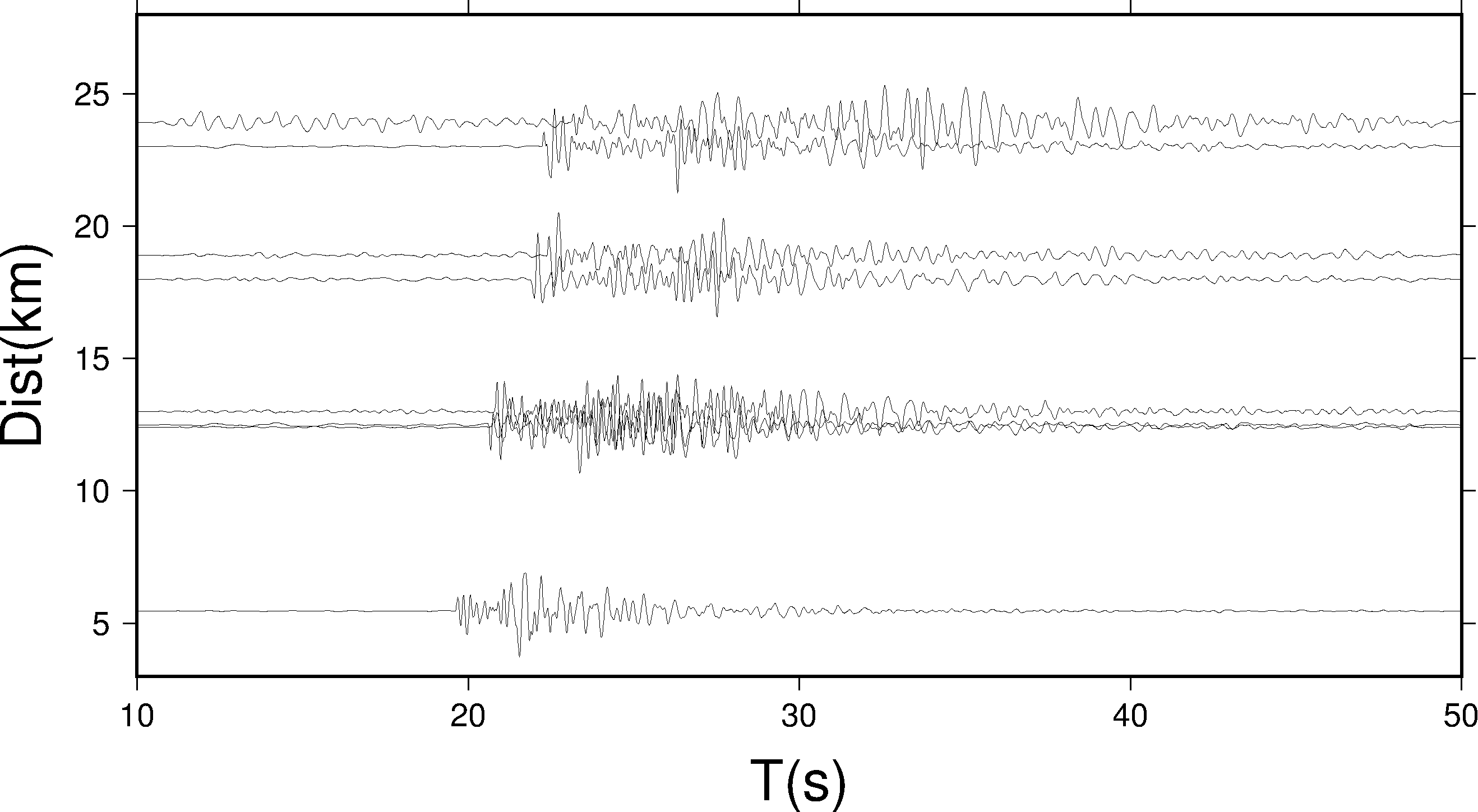
时间轴对齐方式有三种(下面的例子中剖面类型都假定为 k ):
-Ekt表示按照绝对时间对齐-Ektn表示按照某个头段对齐-Ekvel表示按照给定的视速度对齐
说明:
n 可以取值为 - 5,-3,-2 以及 0 到 9
- -5 表示按照文件开始时间(b)对齐
- -3 表示按发震时刻(o)对齐
- -2 表示按初至到时对齐(a)对齐
- 0 到 9 表示按照 t0-t9 对齐
- 若 n 取数字,则等效于不指定 n,即
-Ekt-8等效于-Ekt
按照视速度对齐的代码是
t -= fabs(h.dist)/reduce_vel
下面的例子中展示了按照 b 值对齐,按照 a 值对齐,以及按照视速度 7 km/s 对齐的结果,注意其中 - R 选项的区别:
pssac -JX20c/10c -R0/40/0/0.25 -B10:"T(s)":/0.05:"Dist(degree)":WSen -Edt-5 -M0.5 *.z > test.ps
pssac -JX20c/10c -R-15/35/0/0.25 -B10:"T(s)":/0.05:"Dist(degree)":WSen -Edt-2 -M0.5 *.z > test.ps
pssac -JX20c/10c -R10/50/0/0.25 -B10:"T(s)":/0.05:"Dist(degree)":WSen -Ed7 -M0.5 *.z > test.ps
这里只给出 -Edt-2 的绘图结果:
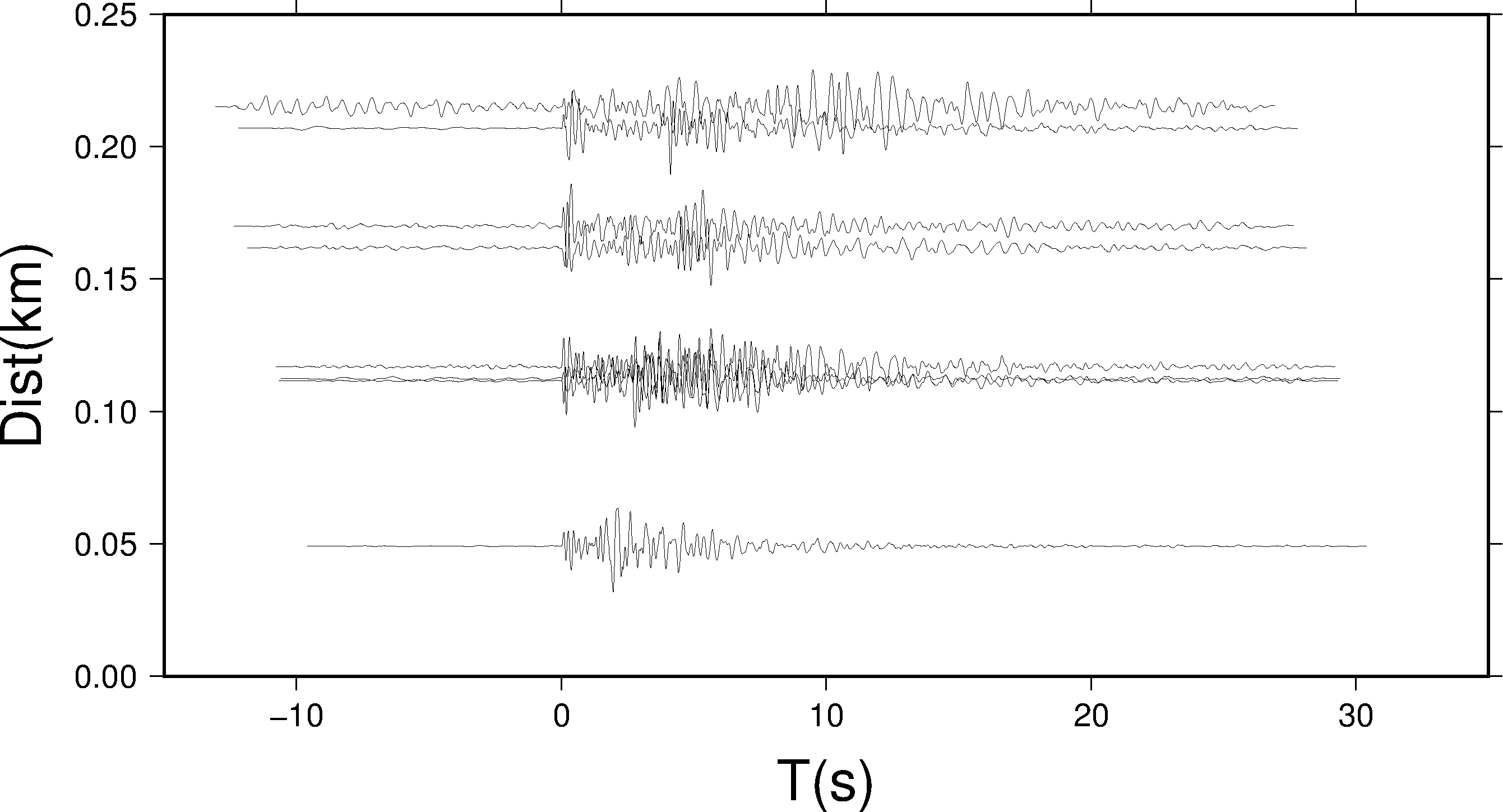
-Edt-2 表示所有的波形要按照头段中的 a 值对齐,此时,波形中 a 所对应的数据点都位于 X 轴的 0 值处。因为数据中 a 大概在 20 秒左右,因而按照 a 值对齐之后,原波形的 X 轴范围 [10,50] 就变成了现在的 [-10, 30] 左右。
-C 选项
由于 -E 的优先级高于 -C 的优先级,故而 - C 中的时间窗要根据对齐后的数据时间轴来选择:
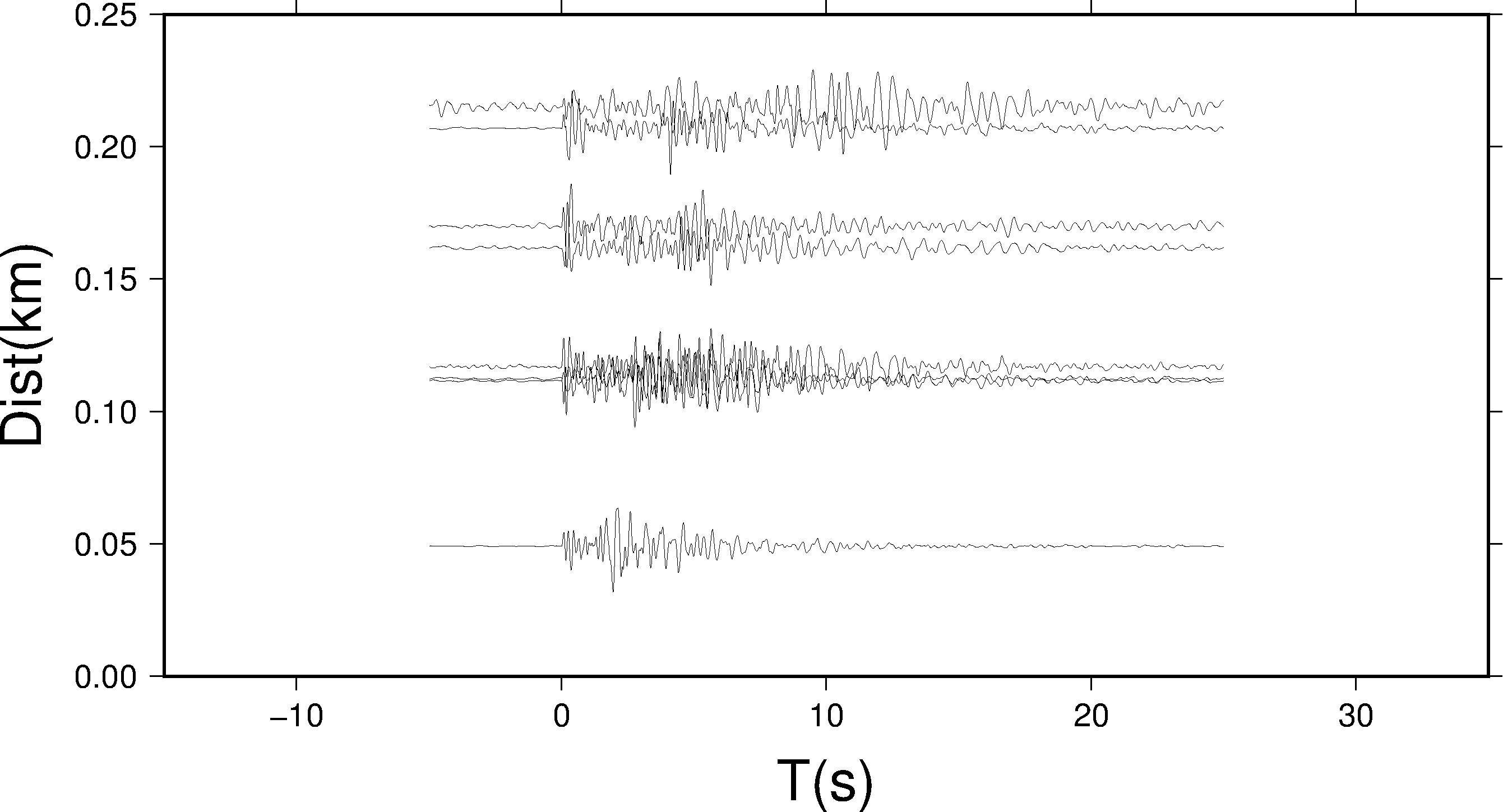
pssac -JX20c/10c -R-15/35/0/0.25 -B10:"T(s)":/0.05:"Dist(km)":WSen -Edt-2 -M0.5 -C-5/25 *.z > a.ps
如下图所示,对齐后的 X 轴范围是 - 15 到 35,此时的截窗范围为对齐后的 - 5 到 25 秒:
任意位置图
pssac 只支持 5 种剖面类型,有时候可能想要绘制其他量的剖面(比如慢度),或者想要在任意位置放置一个波形,或者想要不同波形有不同的画笔属性。这就需要用到 pssac 的另一个功能,即从标准输入中传递数据给 pssac。
要传递给 pssac 的数据有四列,格式为:
sacfile X Y pen
其中 sacfile 为 SAC 文件名,X 为波形起点时刻的 shift 量,Y 为波形在 Y 轴的位置,pen 为画笔属性。
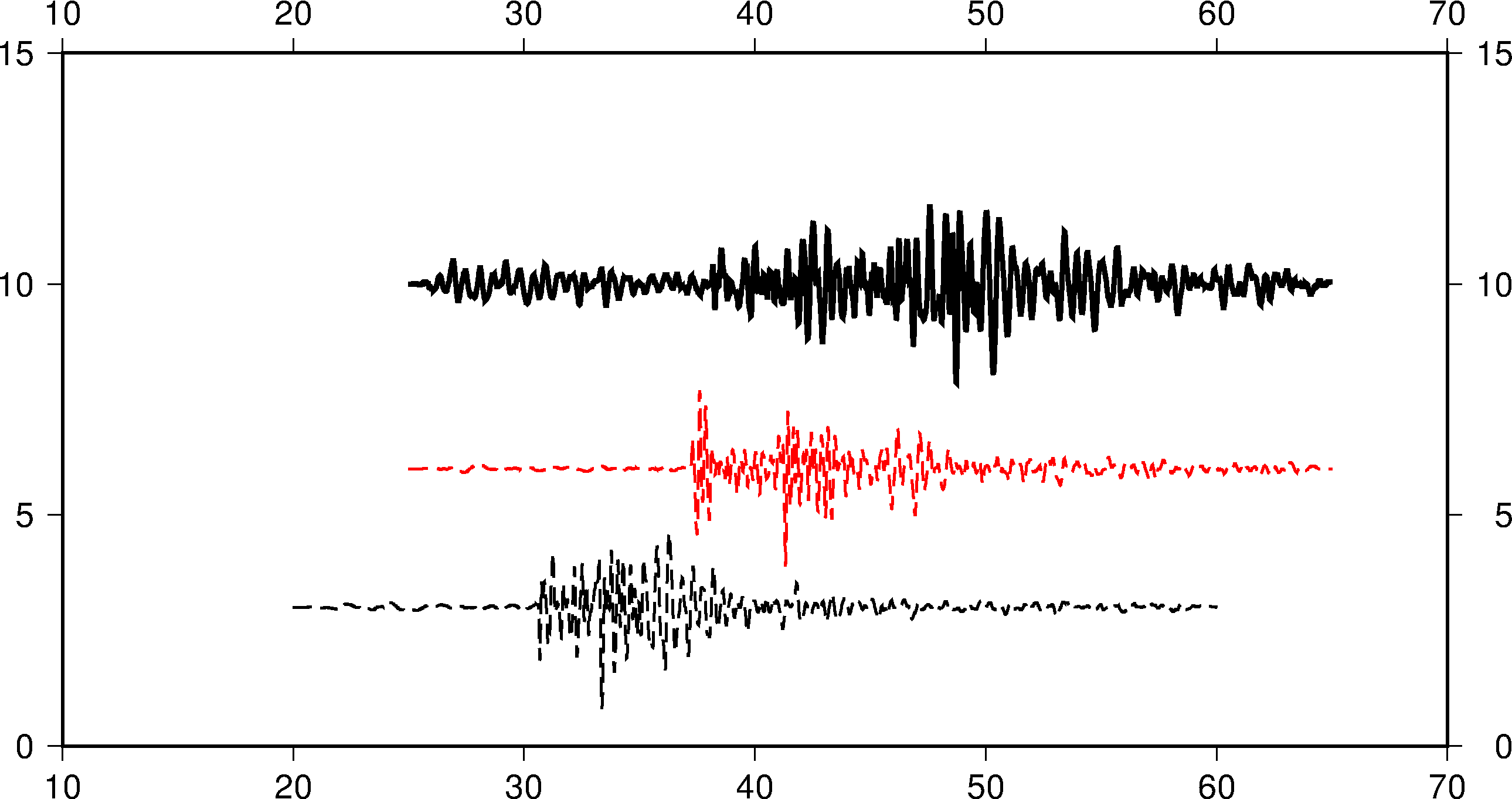
$ pssac -JX20c/10c -R10/70/0/15 -B10/5 -M1 > a.ps << EOF
cal.z 10 3 1p,black,-
cao.z 15 6 1p,red,-
cda.z 15 10 2p,black
EOF
效果图如下:
注意:这一功能不能用于将波形画在地图上。对于地图而言,-R 指定的横轴为经度、纵轴是纬度,而 pssac 中 - R 指定的横轴是时间,纵轴是振幅。对于纵轴,可以使用 -M 选项对振幅进行任意比例的缩放,所以振幅和纬度之间的不一致性是可以消除的。而对于横轴而言,经度与时间的不一致性却很难消除。因而,想要用 pssac 将波形绘制在地图上,没有一个比较好的解决方案。但对于具体需求而言,是有可能使用某些 “黑科技” 来实现的,这将放在单独的博文中讨论。
其他
这里会介绍算法中的一些细节。
-Msize 归一化
振幅的归一化算法中实际上是将数据的振幅乘以比例因子 yscale,其中:
yscale = size*fabs((north-south))/(h.depmax-h.depmin)/project_info.pars[1])
其中,
north和south为 - R 选项中指定的 Y 轴的最大值和最小值;h.depmax和h.depmin为当前数据的振幅的最大值和最小值;project_info.pars[1]是 - J 选项中当前投影的高度,单位为 inch;
在这个例子中:
pssac -JX6i/5i -R9/20/-2.5/2.5 -B1:"T(s)":/0.5g0.5:"Amplitude":WSen -M2 seis.1 > test.ps
north=2.5 Y; south=-2.5 Y(这里 Y 表示 Y 轴的单位,其物理意义可以是振幅,也可以是震中距等)h.depmax=1.619187 Y; h.depmin=-1.470733 Yproject_info.pars[1] = 5 inchsize = 2 inch
则波形的最大振幅差经过归一化之后为:
(h.depmax-h.depmin) * yscale = size * abs(north-south)/project_info.pars[1]
= 2 inch * (2.5 Y - (-2.5 Y))/5 inch
= 2 Y
即归一化之后的最大振幅差在图上的高度为 2 个 Y 单位。
修订历史
- 2013-08-08:初稿;
- 2015-07-17:将原稿的几篇合并并整理成一篇;
- 2016-03-16:解释了
-E选项中 n 取其他值的含义; - 2016-03-16:修复了图片 Y 轴标签的 bug;Thanks to gwx2013 @ USTC;
文章作者 SeisMan
上次更新 2015-07-17