fk 用法笔记
文章目录
fk 是 Prof. Lupei Zhu 写的一个用于计算 水平分层模型 下的理论格林函数并合成 理论地震图的代码包。代码是开源的,可以直接编译使用。
代码中包含了如下几个重要的命令/脚本:
fk:用于计算格林函数的主程序;st_fk:用于计算静态格林函数的主程序;trav:用于计算 P、S 初至到时的辅助程序;sachd:用于修改 SAC 头段的辅助程序;fk.pl:对fk、st_fk、trav和sachd的封装,一般情况下直接使用fk.pl脚本即可;syn:用于将格林函数合成为理论地震图三分量的程序;fk2mt:将FK生成的格林函数转换为另一种Moment Tensor格式的格林函数,即Moment Tensor的每个分量分别对应3个格林函数;
因而,实际操作的时候,只需要调用 fk.pl 生成格林函数,再调用 syn 将格林函数合成为三分量地震图即可。
相关文献
- Haskell (1964), BSSA
- Wang and Herrmann (1980), BSSA
- Takeuchi and Saito (1972), Methods in Computational Physics
- Zhu and Rivera (2002), GJI
建议的阅读方式:
- 若想了解
fk.pl中每个选项的含义,阅读 Zhu and Rivera (2002) 以及本文就差不多了; - 若想理解代码的实现细节,则需要在 Zhu and Rivera(2002) 的基础上,阅读其余三篇文章,至少要阅读 Haskell (1964)。
需要注意的一点是,这几篇文献虽然说的都是同一种方法,但在很多东西的定义上是有区别的,所以在推导代码中的公式时应以 Zhu and Rivera (2002) 为准。Zhu and Rivera (2002) 区别于前面其他文献的地方主要在于,重新定义了传播矩阵,并将静态解与动态解统一到同一个公式中。
基础原理
这里不涉及算法的细节,只介绍一些基础的东西。
根据 Zhu and Rivera (2002),在定义了柱坐标系之后,位移可以表示为:
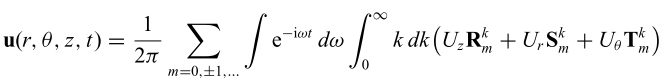
公式中涉及到了一个求和与两个积分:
- 对频率的积分,本质上就是一个反傅里叶变换,技术上很成熟了,可以不管
- 对 m 的求和,其实是对方位角模数的求和,理论上是要从零求和到无穷的。但是由于震源的简单性,只需要对几项做求和即可,具体的求和数目由震源类型决定:
- 爆炸源:m=0
- 单力源:m=0, 1
- 双力偶:m=0, 1, 2
- 对 k 的积分是一个难点,只能进行数值积分,由于积分核 $U_z R_m^k + U_r S_m^k + U_{\theta} T_m^k$ 比较复杂,在做数值积分的时候就需要更多的考虑。
积分核 $U_z R_m^k + U_r S_m^k + U_{\theta} T_m^k$ 中 R、S、T 是柱坐标下的基矢量,由一堆 Bessel 函数组成,已知。该算法中的一大堆数学推导以及细节都是为了求出 Uz、Ur 和 Ut。具体 Uz、Ur 和 Ut 怎么求,不是本文的重点,需要了解的只能自己推公式。
参数说明
先把用法贴在这里作为参考:
fk.pl -Mmodel/depth[/f_or_k] [-D] [-Hf1/f2] [-Nnt/dt/smth/dk/taper]
[-Ppmin/pmax[/kmax]] [-Rrdep] [-SsrcType] [-Uupdn] [-Xcmd] distances
速度模型
-Mmodel/depth/k_or_f 中的 model 为模型文件名, k 和 f 的作用在下面会解释。
格式
fk 的输入速度模型是一维水平分层速度模型,其格式为:
thickness vs vp/vs [rho Qs Qp]
或:
thickness vs vp [rho Qs Qp]
其中
- 列 1:该层的厚度(km) 注意是厚度不是深度
- 列 2:S 波速度(km/s)
- 列 3:波速比或 P 波速度
- 列 4:密度( $g/cm^3$ )
- 列 5:S 波的 Q 值
- 列 6:P 波的 Q 值
其中前三列是必须的,若未指定密度,则使用经验公式 rho=0.77+0.32*vp;若未指定 Qs,则取 Qs=500;若未指定 Qp,则取 Qp=2*Qs。
关于 k 和 f
- 若命令行中使用
-Mmodel/depth,则表示输入模型为第二种格式; - 若命令行中使用
-Mmodel/depth/k,则表示输入模型使用第一种格式,即第三列是波速比; - 若命令行中使用
-Mmodel/depth/f,则表示需要对速度模型做展平变换,当震中距较大时需要这样做;
备注
fk.pl的输入模型是先 Vs 再 Vp,而fk.pl在调用fk时使用的模型是先 Vp 后 Vs,注意不要搞混;- 若第一层的厚度为零,则该行指定了上半空间的参数;
- 若第一层的厚度不为零,则上半空间为真空,该层给出了地表下方第一层的参数;
- 最后一层会被自动当做下半无限半空间,并修改其厚度为 0;
- 对于液态层(如海水和外核):
- S 波速度可以用零表示,程序中用自动用 0.0001 替换零值;
- Qs 值不可以取为零,应取某小值;
震源
震源深度
震源深度由 -Mmodel/depth/[f_or_k] 中的 depth 指定,单位为 km。
需要注意,震源深度不能位于速度模型的分界面上,即震源的深度必须位于模型某层的内部。 fk 在做展平变换时,震源和速度模型的分界面的深度所用的转换公式不同,所以,当使用了展平变换,即便震源深度和界面深度相同,程序也不会报错。 这一点实际使用时要注意(尽管没有报错,也不能让震源在界面上)。
大多数计算理论地震图的方法都会有这样的限制,因为在计算过程中会用到震源所在层的速度或密度,若震源位于速度模型的分界面上,则会出现参数的间断。
震源类型
fk 中用 -SsrcType 指定震源类型,其中 srcType 可以取如下三个值:
- 0:爆炸源;
- 1:单力源;
- 2:双力偶源;
台站
台站深度
-Rrdep 中 rdep 用于设置 receiver 的深度(单位为 km),默认值为零,即台站位于地表。
需要注意,fk 中要求震源和台站不能位于同一深度。代码中,会计算震源和台站之间的深度差 hs,并将其作为分母。但这一限制的本质原因尚不清楚。
台站震中距
fk.pl 命令行中可以指定多个震中距,震中距的默认单位为 km。
当震中距较大时,以 km 做单位很不方便,此时可以使用 -D 选项,表明震中距的单位为度。同时,由于震中距比较大,此时可能还需要对速度模型做展平变换。
震中距可以是 0。
时间序列
说说 -Nnt/dt/smth/dk/taper 中的 nt、dt 和 smth。
采样间隔
dt 即生成的格林函数的采样间隔。与此同时,dt 决定了 fk 要计算的最高频率,其公式为
$$f_{max} = \frac{1}{2 dt}$$
即 fk 生成的格林函数的最高频率是由 dt 决定的 Nyquist 采样率。
因而,一般来说,要首先根据自己的实际需求,确定所需要的最高频率,进而决定 dt 。
数据点数
nt 即数据点数,nt 的选择有一些需要注意的地方:
- nt 必须为 2 的 n 次方,即可以取 1、2、256、512、1024 等。程序中限制了
nt*smth不得超过 8192。若想要突破数据点数的限制,可以增大源码model.h中nt=8192的值。- nt=1,则调用
st_fk直接计算静态位移解; - nt=2,则调用
fk计算零频位移,等效于静态位移解; - nt 必须为 2 的 n 次方是因为在 FFT 时数据点为 2 的 n 次方时有快速算法;
- nt=1,则调用
- $T=nt*dt$ 确定了最终数据的总长度
smooth 因子
由于 dt 决定了 fk 计算的最高频率,所以 dt 是不能随便取的。比如需要最高频率为 2.5Hz,则 dt 应取 0.2s,但是若希望最终生成的数据的采样间隔为 0.05s,则需要 smth 这个参数。
在程序中,smth 做了两件事情:
- 将 dt 除以 smth;
- 将总数据点数乘以 smth;
总的效果应该相当于对计算结果做了一个插值,这也可以通过 SAC 的插值命令来完成。在程序实现时,实际上就是在反傅里叶变换之前,给数据的高频部分补上更多的零值。
同样由于快速傅里叶算法的限制, smth 也必须取 2 的 n 次方。
频率
最高频率
前面已经说到,fk 所计算的最高频率由 dt 决定:
$$f_{max} = \frac{1}{2 dt}$$
频率间隔
频率域的采样间隔(分辨率)为 $df=\frac{1}{T}=\frac{1}{nt*dt}$
高通滤波
fk 会从零频开始,以 df 为频率间隔,一直到最高频率 fmax,计算每个离散频率处的值。
比如,给定参数 dt=0.1,npts=1024,则 fk 计算的最高频率为 5 Hz,频率间隔 df 约等于 0.01Hz。因而 fk 会计算 0 Hz、0.01 Hz、0.02 Hz 一直到 5 Hz 的值,共计循环 512 次。
有些情况下,比较低频的信息是没有用的,所以可以不必计算,这样循环可以进一步减小,以加速计算。
-Hf1/f2 中, f1 限定了循环过程中频率的下限,即对频率的循环会从 f1 开始计算到 fmax 而不是从零开始,这本质上是一个高通滤波器。
这样一来,fk 会计算频率在 f1 和 fmax 之间的值,对于小于 f1 以及大于 fmax 的频率段,其值直接设为零。这实际上是在频率域直接截断,似乎会出现一些问题,所以一般都会对频率的两端做尖灭处理,即 f2 和 taper。程序会在 f1 和 f2 之间以及 (1-taper)*fmax 和 fmax 之间分别加上余弦窗。
taper 的默认值为 0.3,所以当 dt=0.1s 时,fmax=5Hz,则在 3.5Hz 到 5Hz 之间会加上余弦窗,此时数据的频段上限是 5Hz 还是 3.5Hz 呢?这是个疑问。
k 积分
k 是什么
这里的 k 不是波数,而是水平波数:
$$k = k_x = \vec{k}\cdot \vec{x} = \frac{\omega}{v} \sin \theta = \omega p$$
其中, $\theta$ 是射线与垂直方向的夹角, $p=\frac{\sin \theta}{v}$ 是水平慢度,也就是射线参数。
下限和上限
-Ppmin/pmax[/kmax] 可以限定 k 积分的上下限。其中 pmin 确定了 k 积分的下限:
$$k_{min} = \omega pmin$$
pmax 和 kmax 决定了 k 积分的上限:
$$k_{max} = \sqrt{kmax^2+\omega pmax}$$
说明:
- pmin 和 pmax 的取值范围是 0 到 1,代码中会将 pmin 和 pmax 都除以震源处的 S 波速度。
- 程序中
kmax=kmax/hs,其中 hs 是震源与台站的深度差;由于积分核在零频处以 exp(-k*hs) 的速度随着 k 衰减,因而要求 kmax>10,以保证求和足够多。 - 指定了 pmin 和 pmax,就相当于指定了射线参数的范围,或射线出射角度的范围,似乎可以用于筛选中特定射线参数范围的射线;
- 为什么 pmin 和 pmax 在程序中都要除以 S 波速度呢?这样当给定 $pmin=\sin 30=0.5$ 时,以 30 度角出射的 S 波会被计算,而以 30 度角出射的 P 波则不会被计算?这样对吗?
- pmin 和 pmax 的取值为 0 到 1,为什么不是 - 1 到 1?也许正负号是由
updn决定的。
上行和下行
-Uupdn 选项可以指定是计算全波场还是只计算上行波或下行波。updn 可以取值如下:
- 0:计算全波场;也是默认值;
- 1:仅计算下传波场;
- -1:仅计算上传波场;
该参数取不同的值,会影响到程序内部的一些公式。具体的原理可能需要推公式才能理解。
dk
dk 用于控制 k 积分的积分间隔。程序中 $dk=dk*PI/max(x,hs)$,其中 hs 为震源与台站的深度差, x 为震中距,因而 k 积分间隔实际上是与要计算的最大震中距有关的。
由于积分核中 J(kx) 在大震中距时按 2pi/x 的周期震荡,因而要求 dk 小于 0.5,以保证每个周期内至少有四个采样点。官方建议取值为 0.1 到 0.4。dk 理论上越小越好,当然 dk 越小计算就会越慢。
振幅压制
这个参数在 fk.pl 脚本内部可以修改,但是在命令行里没法修改。
对于实序列 $f(t)$ ,其傅里叶变换为:
$$F(\omega) = \int f(t) e^{-i\omega t} dt$$
若将该实序列 f(t) 乘以 $e^{-\sigma t/T}$,即 $g(t)=f(t)e^{-\sigma t/T}$ 的傅里叶变换为:
$$G(\omega) = \int g(t) e^{-i\omega t} dt = \int f(t) e^{-\sigma t/T} e^{-i\omega t} dt = \int f(t) e^{-i(\omega-i\sigma/T)} dt = F(\omega-i\sigma/T)$$
因而,在频率域将 $\omega$ 减去 $i\sigma/T$ ,相当于对实序列乘以 $e^{-\sigma t/T}$ 。
其中 T 为实序列的总时间长度,sigma 称为压制因子,用于降低数据尾部的振幅值,而最终反傅里叶变换得到的实序列,会再次乘以 $e^{+\sigma t/T}$,以消除压制因子对振幅的影响。所以,理论上看,sigma 没什么实际用途,这样处理的具体目的还不清楚,似乎是出于频率域的稳定性考虑的。
DEBUG
fk 提供了 -X 选项用于 debug,最常见的用法是 -Xcat,此时 fk.pl 中 cmd 被替换成 cat 命令,即将所有的输入都传递给 cat 命令,这样可以很清楚地知道要传递的数据是否正确,方便 debug。
格林函数
fk 将生成的格林函数以 SAC 格式写到磁盘中。
爆炸源
生成三个分量,命名为 xxxx.grn.[a-c] ,分别是 Z、R、T 向的格林函数。其单位为 10^-20 cm/(dyne cm) 。
单力源
生成六个分量,其中:
xxxx.grn.[0-2]:m=0 对应的 ZRT 格林函数,等效于 垂直向上 的单位单力产生的位移三分量;xxxx.grn.[3-6]:m=1 对应的 ZRT 格林函数,等效于水平单力产生的位移三分量;
格林函数的单位为 10^-15 cm/dyne 。
双力偶
生成九个分量,其中
xxx.grn.[0-2]:m=0 阶源生成的 ZRT 格林函数,相当于 45-down-dip(DD) 双力偶源在 45 度方位角处产生的位移,并乘以(-2,-2,0)xxx.grn.[3-5]:m=1 阶源生成的 ZRT 格林函数,相当于 vertical dip-slip(DS) 双力偶源在 45 度方位角处产生的位移,并乘以 $-\sqrt 2$xxx.grn.[6-8]:m=2 阶源生成的 ZRT 格林函数,相当于 vertical strike-slip(SS) 双力偶源在 22.5 度方位角处产生的位移,并乘以 $-\sqrt 2$
格林函数的单位为 10^-20 cm/(dyne cm) 。
说明
在大多数教程以及文献中,任意一个双力偶源可以表示为三个基本断层的线性迭加。这三个基本断层分别为 DD、DS 和 SS。有些计算格林函数的代码会计算出三种基本断层的位移解,然后根据文献中给出的辐射花样系数进行合成。而 fk 计算出的是 m=0、1、2 时的位移解,虽然这三者分别与 DD、DS、SS 在某个特定方位角的位移解有关系。因而在对 fk 生成的格林函数进行合成时,有专门的辐射花样系数,参见 Zhu and Rivera(2002) 的附录 B10-B12。
syn 用法说明
fk.pl 只是算出了格林函数, syn 的作用在于将格林函数组合起来得到RTZ三个方向的理论地震图。
syn 的用法相对比较简单,此处作简单介绍:
-M选项指定震源机制信息,有四种用法:对于爆炸源:
-Mmag其中 mag 的单位是 dyne-cm对于单力源:
-Mmag/strike/dip其中 mag 的单位是 dyne, dip为力的方向相对于水平方向的夹角- dip=0: 水平单力
- dip=90: 垂直向下单力
- dip=-90: 垂直向上单力
对于双力偶源:
-Mmag/strike/dip/rake其中 mag 是矩震级Mw,strike/dip/rake 的定义参照 Aki&Richards(1980)对于地震矩源:
-Mmag/Mxx/Mxy/Mxz/Myy/Myz/Mzz其中 mag 的单位是 dyne-cm。此处有大坑,见后面的详细说明。
-Aazimuth选项指定台站方位角,定义为相对于北方向顺时针旋转的角度-Ddura/rise指定一个梯形作为震源时间函数。其中 dura 是梯形震源时间函数的总持续时间,rise 代表了梯形中上升段所占据的时间比例,取值范围为0到0.5,若取值为0.5,则梯形退化为三角形-SsrcFunctionName除了使用 -D 选项之外,也可以使用将一个SAC文件作为震源时间函数。-S选项后直接跟SAC文件名。用SAC文件作为震源时间函数时需要注意两点:
- SAC文件的采样间隔要与格林函数的采样间隔相等。如果不等也没关系,但要注意 syn 是直接把数据点卷积格林函数的,并没有考虑采样间隔的问题,因而若采样间隔不等可能会一些易忽略的错误;
- 严格的震源时间函数应该满足积分之后最大值等于1,只有这种情况下,震级或震源强度的定义才是准确的。当然,若无需考虑绝对振幅是否正确的问题,震源时间函数可以不满足这一要求。
-Ff1/f2/n对理论地震图进行滤波-GFirstCompOfGreen指定第一个FK格林函数的文件名-TFirstCompOfGreen指定第一个MT格林函数的文件名。MT格林函数是指矩张量的每个分量所对应的格林函数,共计6*3=18个。程序fk2mt可以将FK生成的FK格林函数转换为这里所需的MT格林函数其他选项都很简单,就不介绍了
关于地震矩源 -Mmag/Mxx/Mxy/Mxz/Myy/Myz/Mzz,需要注意:
- 此处x=North、y=East、z=Down,即地震矩张量使用的是NED坐标系
- GCMT网站上给出的地震矩张量是RTP坐标系,二者之间的转换公式见 Aki&Richards(1980)P117 Box4.4
- GCMT网站中地震矩张量的6个分量的顺序是 Mrr Mtt Mpp Mrt Mrp Mtp,而本程序中的顺序是 Mxx Mxy Mxz Myy Myz Mzz,因而若使用GCMT的震源机制解,则需要对6个分量进行坐标转换并修改其先后顺序
输出类型
fk 计算得到的格林函数究竟是什么物理量呢?是位移还是速度?
在 Zhu and Rivera(2002) 的文章中、代码中的注释以及说明文档等多个地方都提到 fk 计算出的是位移量,而实际上利用 fk 和 syn 计算出来的合成地震图是速度场。
Zhu and Rivera(2002) 的附录 B 中给出了不同震源类型以及不同 m 值所对应的 source term,这里的 source term 代表了震源引起的位移-应力不连续。source term 是一个与频率无关的常数,所以 fk 中所使用的 source term 在时间域上的脉冲源。(时间域上的脉冲函数,在频率域是一个常数,所以 fk 中在频率域加了一个常数的 source term,实际上相当于在时间域上加上脉冲源。)
因而,fk 实际上计算的是脉冲源对应的位移场,其等效于阶跃函数所产生的速度场。(阶跃函数的偏导即脉冲函数。)
对于一个真实的小震级的简单地震而言,其震源时间函数可以认为是一个阶跃函数,震源时间函数的偏导就是脉冲函数。因而 fk 计算出的格林函数实际上是速度场,在使用 syn 合成真实数据时,如果使用 -D 选项指定了一个三角震源函数(近似的脉冲函数),得到的合成数据都是速度场。
其他说明
- 对于 PREM 模型,震源深度取 15km,震中距为 5 度,做不做展平变换,震相的走时差大概在 0.8s 左右
- 将 PREM 模型离散成每层 20km 或 50km,计算出的结果差异不大
- 若台站深度大于震源深度,则会对模型做翻转,程序中的部分参数乘以 - 1;
fk.f中输入的src_layer表示震源位于第src_layer层的顶部,rcv_layer同理;而trav中src_layer表示震源位于第src_layer的底部;- 输出的格林函数文件中
xxx.grn.0和xxx.grn.5会包含 P 波和 S 波的到时。如果 syn 合成的是 Double Couple,则合成的理论地震图里会包含 P 波和 S 波的到时。如果 syn 合成的是 ISO,则合成的理论地震图里没有到时。
疑问
- 在考虑衰减时,Aki and Richard(1980)的公式 (5.88) 中给出的公式中虚数前为负号,而 fk 代码中为正号。Why?
- 如何从数学或物理上详细解释
sigma的含义?
修订历史
- 2015-02-28:初稿;
- 2017-01-09:增加了 syn 的使用说明;
文章作者 SeisMan
上次更新 2017-10-28