地震学中的坐标系
文章目录
地震学中不同的作者定义了不同的坐标系,搞清楚各个坐标系的定义可以避免使用过程中出现错误。
三分量波形数据坐标系
通常,地震仪记录的是ZNE方向的三分量波形数据。实际研究中,经常会需要旋转到ZRT坐标系或者LQT坐标系。下面介绍一下各个坐标系的定义。
NEZ坐标系
NEZ 是最简单也是最常见的坐标系。
- N: 正北方向为正方向
- E: 正东方向为正方向
- Z: 垂直向上为正方向
对于 Z 方向,可能存在向上为正还是向下为正的问题。SEED标准中规定垂直向上为正方向,详见 SEED Reference Manual v2.4 P68 中的说明。
因而NEZ构成了一个左手坐标系。
RTZ坐标系
RTZ的定义如下:
- R: R方向定义为从震中位置沿着大圆路径指向台站的方向
- T: T方向垂直于R和Z方向所构成的平面,且选取的T轴正方向使得RTZ构成了左手坐标系
- Z: 垂直向上为正方向
如图所示:
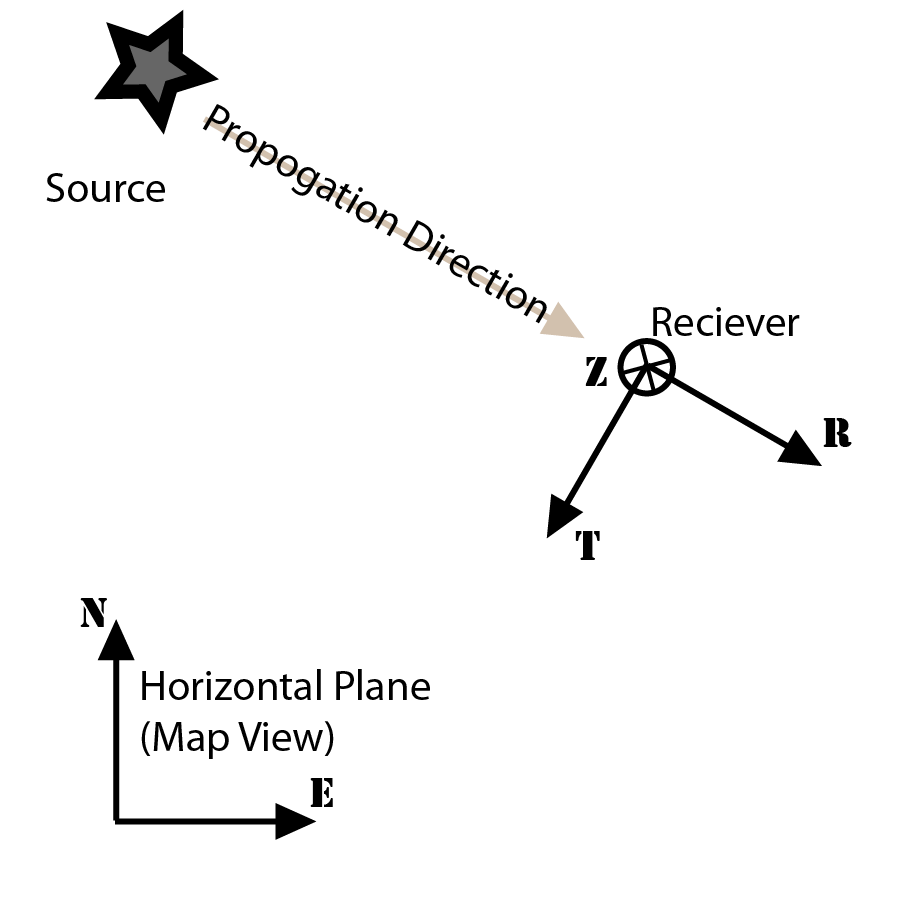
NEZ坐标系到RTZ坐标系的转换公式为
其中 $\alpha$ 是 R 方向与 N 方向的夹角,也就是反方位角加180度。
LQT坐标系
LQT坐标系的定义如下:
- L: P波偏振方向
- Q: SV波偏振方向
- T: SH波偏振方向,与 RTZ 坐标系中T的定义相同
| 垂直面视角 | 水平面视角 |
|---|---|
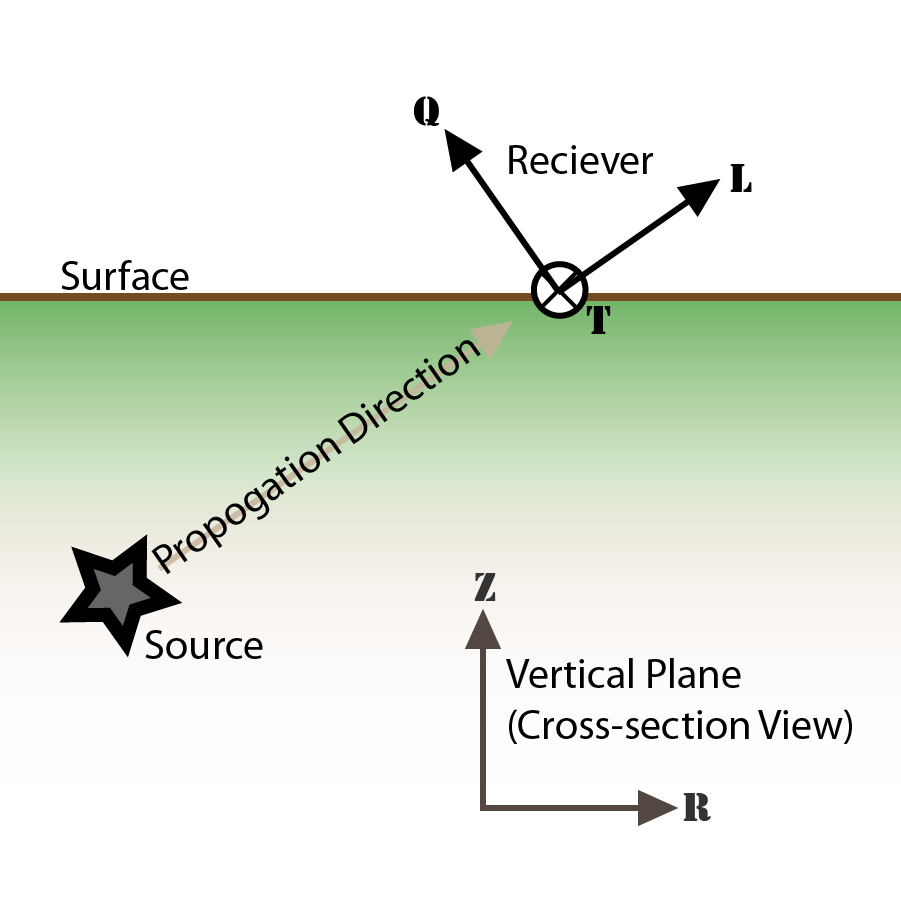 | 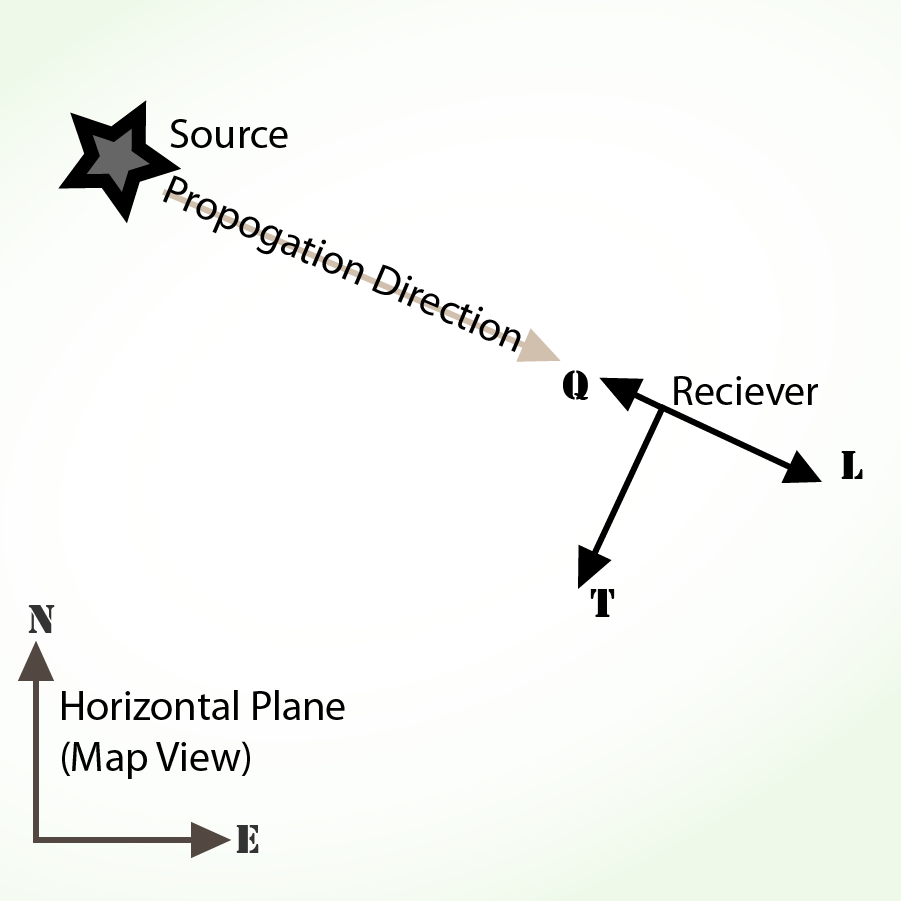 |
可以先将NEZ坐标系转换为RTZ坐标系,再根据P波入射角将RZ两个方向旋转到LQ方向即可。当然也可以直接通过三维旋转将NEZ旋转到LQT坐标系。
地震矩张量张量坐标系
地震矩张量是一个3X3的矩阵,通常写为
由于具有对称性,因而地震矩张量只有6个独立的量,即
有时候会将这6个量写成数组而不是矩阵的形式,通常顺序是这样的:
Mxx Myy Mzz Mxy Mxz Myz
在不同的坐标系下,XYZ分别代表不同的方向。
NED 坐标系
NED 坐标系在 Aki & Richards (1980) 中有详细定义,即:
- X=North
- Y=East
- Z=Down
如下图所示:
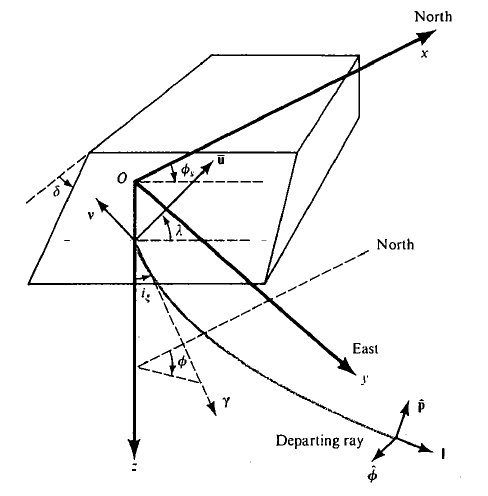
USE/RTP 坐标系
USE 坐标系的定义为:
- X=Upper
- Y=South
- Z=East
USE 坐标系还有很多别名,比如:
GlobalCMT 所使用的坐标系称为RTP坐标系,RTP坐标系其实就是USE坐标系。
- X=R=Upper
- Y=T=South
- Z=P=East
在GMT的psmeca中,RTP坐标系也称为RTF坐标系
在Aki&Richards(1980)中,RTP坐标系写作 $r\Delta\phi$ 坐标系
Aki&Richards (1980) P118 给出了USE/RTP坐标系与NED坐标系之间的转换关系:
参考
文章作者 SeisMan
上次更新 2017-01-12