辐射花样的计算与震源球的绘制
文章目录
P 波辐射花样计算公式
Quantitative Seismology (Aki and Richards,1980) 中式(4.29)给出了零迹地震矩 M 所产生的 n 分量位移公式:
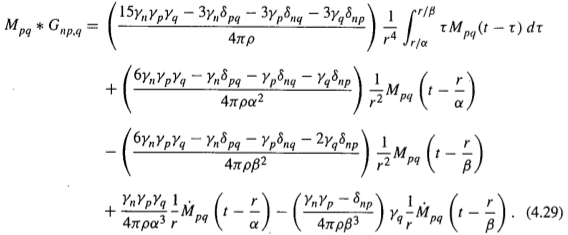
其中等式右边共计 5 项,第一项为近场项,第二、三项分别是 P、S 波的中间场项,第四、五项分别为 P、S 波的远场项。一般研究辐射花样大多关注于 P 波远场辐射花样,即第四项。
式(4.91)中给出了远场 P 波位移的矢量形式,看上去更加直观一些:
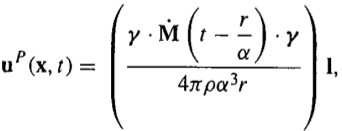
其中,除去震源时间函数以及绝对振幅,只留下辐射花样相关的因子:
$$Rad = \mathbf{\gamma} \cdot \mathbf{M} \cdot \mathbf{\gamma}$$
其中,$\mathbf{\gamma}$ 为离源矢量,是离源角和方位角的函数,表征了地震射线从震源的出射方向,$\mathbf{M}$ 为矩张量。
坐标系的选取
对于点源而言,上式中的矩张量是一个常量(M(t) 与时间相关的部分可以分离成震源时间函数),离源矢量是与方位角和离源角有关的矢量,所以求辐射花样的本质就是矢量和张量的乘法。如何选定坐标系是一个关键问题。
按照 Aki&Richards(1980) 中图 4.20 的方式定义坐标系,如下图,定义 X 轴为北向,Y 轴为东向,Z 轴为垂直向下,即 NED 坐标系。
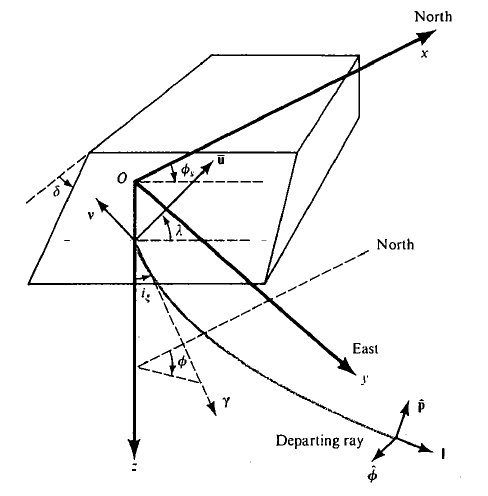
可以得到,此坐标下,离源矢量 $\mathbf{\gamma}$ 的具体形式:
震源机制解
震源机制解一般有两种表达方式,一种是矩张量形式,另一种是断层参数形式。
- 矩张量形式是震源机制的通用表示方式,需要六个分量。对于地震震源而言,多限制矩张量为零迹张量,即去除爆炸源的成分,只保留 double couple 和 CLVD 部分。
- 断层参数形式需要三个分量 (strike,dip,rake),只能表示 double couple 位错源。
Global CMT 给出了零迹矩张量解和断层参数解。
若使用 GCMT 给出的断层参数 (strike,dip,rake) 解,则可根据 Aki&Richards(1980) P117 Box4.4 中式 1 将其转换成 NED 坐标系下的矩张量。
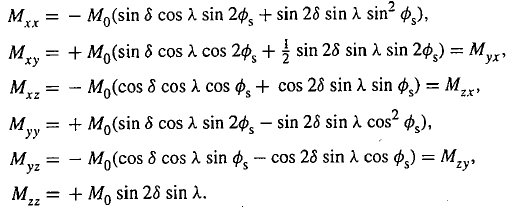
若使用 GCMT 给出的矩张量解,由于 GCMT 给出的是 (Mrr, Mtt, Mff, Mrt, Mrf, Mtf) 解,即 USE 坐标系下的矩张量,需要转换成 NED 坐标系的矩张量,方可使用。转换公式如下:
不同的文献给出的坐标系可能不同,比如这里提到的 NED 坐标系和 USE 坐标系。即便相同的坐标系所使用的符号也可能不同,比如 GCMT 的 $(r,t,f)$ 坐标系和 Aki&Richards(1980) 中给出的 $(r,\Delta,\phi)$ 坐标系其实都是 USE 坐标系。
辐射花样计算代码
获得矩张量以及离源矢量的表达式之后,即可求出震源球上任一点的辐射振幅。代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define PI 3.14159265358979323846
#define DEG2RAD PI/180.0
int main (int argc, char *argv[]) {
int i, j;
float m[3][3];
if (argc != 7 && argc != 4) {
fprintf(stderr,"Usage: %s mrr mtt mff mrt mrf mtf\n", argv[0]);
fprintf(stderr," Or: %s strike dip rake\n", argv[0]);
exit(1);
}
if (argc == 7) { // moment tensor
sscanf(argv[1], "%f", &m[2][2]); // mrr -> mzz
sscanf(argv[2], "%f", &m[0][0]); // mtt -> mxx
sscanf(argv[3], "%f", &m[1][1]); // mff -> myy
sscanf(argv[4], "%f", &m[2][0]); // mrt -> mzx
m[0][2] = m[2][0];
sscanf(argv[5], "%f", &m[2][1]); // mrf -> -Mzy
m[2][1] = -m[2][1];
m[1][2] = m[2][1];
sscanf(argv[6], "%f", &m[0][1]); // mtf -> -Mxy
m[0][1] = -m[0][1];
m[1][0] = m[0][1];
} else if (argc == 4) { // strike, dip, rake
float strike, dip, rake;
sscanf(argv[1], "%f", &strike);
sscanf(argv[2], "%f", &dip );
sscanf(argv[3], "%f", &rake );
strike *= DEG2RAD;
rake *= DEG2RAD;
dip *= DEG2RAD;
m[0][0] = - sin(dip)*cos(rake)*sin(2*strike)
- sin(2*dip)*sin(rake)*sin(strike)*sin(strike);
m[0][1] = sin(dip)*cos(rake)*cos(2*strike)
+ 0.5*sin(2*dip)*sin(rake)*sin(2*strike);
m[0][2] = -cos(dip)*cos(rake)*cos(strike)
- cos(2*dip)*sin(rake)*sin(strike);
m[1][1] = sin(dip)*cos(rake)*sin(2*strike)
- sin(2*dip)*sin(rake)*cos(strike)*cos(strike);
m[1][2] = -cos(dip)*cos(rake)*sin(strike)
+ cos(2*dip)*sin(rake)*cos(strike);
m[2][2] = sin(2*dip)*sin(rake);
m[1][0] = m[0][1];
m[2][0] = m[0][2];
m[2][1] = m[1][2];
}
fprintf(stdout," / %6.3f %6.3f %6.3f \\ \n", m[0][0], m[0][1], m[0][2]);
fprintf(stdout,"M = | %6.3f %6.3f %6.3f | \n", m[1][0], m[1][1], m[1][2]);
fprintf(stdout," \\ %6.3f %6.3f %6.3f / \n", m[2][0], m[2][1], m[2][2]);
FILE *fop;
fop = fopen("pattern.dat", "wb");
double az, theta;
float p[3]; // 离源矢量
for (i=0; i<3600; i++)
for (j=0; j<=900; j++) {
az = (double)i / 10.0 * DEG2RAD; // 方位角
theta = (double)j/10.0 * DEG2RAD; // 离源角,仅计算下半球
p[0] = (float)(sin(theta)*cos(az));
p[1] = (float)(sin(theta)*sin(az));
p[2] = (float)(cos(theta));
int k, l;
float amp = 0.0;
for (k=0; k<=2; k++)
for (l=0; l<=2; l++){
amp += p[k]*m[k][l]*p[l];
}
fwrite(&, sizeof(float), 1, fop);
}
fclose(fop);
return 0;
}
此代码可以正确处理断层参数和矩张量两种形式的震源机制解,二者均可被正确转换为 NED 坐标系下的矩张量解。对 360 度的方位角以及 90 度的离源角进行遍历,计算每一点的振幅值,并保存到 pattern.dat 中待用。
关于离源角,需要注意两点:
- 离源角的取值范围为 [0,90],即只计算震源球的下半球,这是因为多数情况下绘制震源球都使用下半球投影(上半球辐射的能量无法传播到大震中距处)。
- 离源角与纬度的对应关系为:纬度 = 离源角 - 90。
震源球的绘制
投影方式的选取
目前已经拥有了震源球的下半球上任意一点的振幅(未归一化),还需要选择合适的投影方式将数据投影到 “赤道” 面上。
绘制震源球有两种投影方式,分别是 Schmidt 投影和 Wulff 投影。前者是等面积投影,后者是等角度投影。在 GMT 中分别对应 JA 和 JS 。这里以 Wulff 投影为例,想要使用 Schmidt 投影只需要把 JS 改成 JA 即可。
绘图脚本
#!/bin/bash
R=0/360/-90/0
J=S0/-90/15c
B=a30f10
name=pattern
PS=${name}.ps
gmt set MAP_FRAME_TYPE=plain
gmt set FORMAT_GEO_MAP=+D
gmt xyz2grd ${name}.dat -G${name}.nc -I6m/6m -R$R -ZLBxf
gmt grd2cpt ${name}.nc -Cpolar -E100 > ${name}.cpt
gmt psxy -R$R -J$J -T -K -P > $PS
gmt grdimage ${name}.nc -R$R -J$J -C${name}.cpt -B$B -BN -K -O >> $PS
gmt grdcontour ${name}.nc -R$R -J$J -L-0.001/0.001 -C1 -K -O -W2p >> $PS
gmt psxy -R$R -J$J -T -O >> $PS
rm gmt.conf gmt.history ${name}.cpt ${name}.nc
绘图脚本的一些说明:
- 设置
FORMAT_GEO_MAP使得方位角范围是 0 到 360,而不是 -180 到 180。其中 0 度指向正北方向。 - 这里 R 的横向范围是 0 到 360,实际上 360 度处与 0 度处是同一个经度,所以网格中没有计算 360 度处的振幅。同时在
-Z选项中使用了 x 以表明 X 轴的周期性。 - 在振幅为 0 处绘制了等值线。
结果展示与比较
震源机制解
从 GCMT 中找到一个地震事件,其机制解如下:
201304191751A SOUTH OF TIMOR, INDONESI
Date: 2013/ 4/19 Centroid Time: 17:51:46.9 GMT
Lat= -12.01 Lon= 121.71
Depth= 29.5 Half duration= 2.0
Centroid time minus hypocenter time: 5.5
Moment Tensor: Expo=24 -1.350 5.410 -4.060 -3.210 -3.580 -0.736
Mw = 5.8 mb = 6.0 Ms = 5.8 Scalar Moment = 6.88e+24
Fault plane: strike=315 dip=45 slip=-12
Fault plane: strike=53 dip=82 slip=-135
矩张量 + Wulff 投影
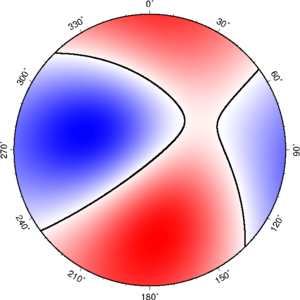
矩张量 + Schmidt 投影
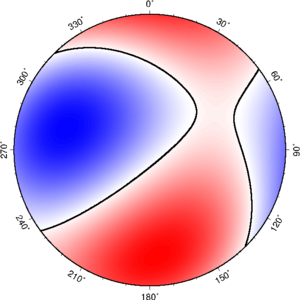
断层参数 + Wulff 投影
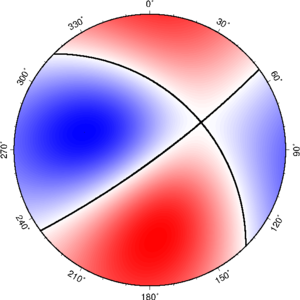
断层参数 + Schmidt 投影
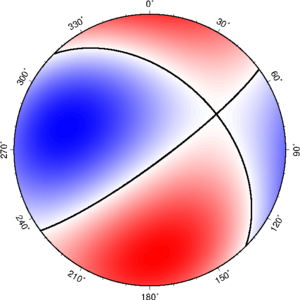
GMT psmeca 绘制矩张量解
psmeca 的 -Sm 选择可以用于在地图上绘制 GCMT 矩张量形式的震源球。需要注意的是这个震源球的投影方式与 J 指定的投影无关。这里把边框画出来,以指示出正北方向。
#!/bin/bash
gmt psmeca -R0/250/-90/90 -JQ22c -Sm7c -W1p -Bx60 -By30 <<EOF> gmt_meca.ps
121.71 -12.01 29 -1.35 5.41 -4.06 -3.21 -3.58 -0.74 24 X Y 201304191751A
EOF

GMT psmeca 绘制矩张量的 double couple 部分
-Sd 用于绘制矩张量的 double couple 部分。
#!/bin/bash
gmt psmeca -R0/250/-90/90 -JQ22c -Sd7c -W1p -Bx60 -By30 <<EOF> gmt_meca.ps
121.71 -12.01 29 -1.35 5.41 -4.06 -3.21 -3.58 -0.74 24 X Y 201304191751A
EOF
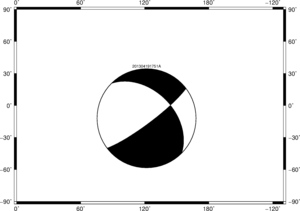
Mopad 绘制矩张量
Mopad 是一个可以计算与绘制矩张量的 Python 脚本,其功能强大,可控制的参数更多:
$ mopad plot -1.35,5.41,-4.06,-3.21,-3.58,-0.74 -i USE
这里 -i USE 指定了输入的六个矩张量分量是 USE 坐标下的解。

图像格式转换
利用 psconvert 命令可以将 PS 文件转换为其它格式的图像,最好选择透明的 PNG 格式:
gmt psconvert -A -TG beachball.ps
一些小结
- 绘制震源球时,选择匹配的坐标系很重要;
- 可以使用 Schmidt 投影和 Wulff 投影绘制震源球,二者大体相同,细节上有差异;
- GMT 的 psmeca 命令使用 Schmidt 投影绘制震源球,这一点无法修改;
- GCMT 给出的震源球精度很低,但可以看出其使用了 Schmidt 投影
JA。
修订历史
- 2014-04-28:初稿 By cxh757;
- 2014-05-01:修订与补充 By SeisMan;
- 2014-05-30:增加了图像格式转换一节;
- 2018-12-20:语法更新为 GMT5;
文章作者 SeisMan
上次更新 2014-05-01